Rozwijanie programu¶

W tym punkcie nauki, po spojrzeniu na kompletną funkcję, powinniście móc powiedzieć co ona robi. Jeżeli dodatkowo robiliście przykłady, sami napisaliście kilka pomniejszych funkcji. W momencie, gdy zaczniecie pisać nieco większe funkcje możecie napotkać nieco większe trudności, w szczególności z błędami pracy programu czy błędami składni.

Aby poradzić sobie ze stale rosnącymi programami, zasugerujemy technikę, zwaną rozwojem przyrostowym. Celem tej techniki jest unikanie długich sesji debugowania poprzez dodawanie oraz testowanie tylko małych kawałków kodu w danej chwili.

Przykładowo załóżmy, że chcemy znaleźć odległość pomiędzy dwoma punktami danymi jako współrzędne (x₁, y₁) oraz (x₂, y₂). Z twierdzenia Pitagorasa wiemy, że ta odległość dana jest poprzez

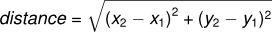
W pierwszym kroku należałoby się zastanowić, jak miałaby wyglądać funkcja distance (odległość) napisana w języku Python. Innymi słowy - jakie mamy dane wejściowe (parametry) i wyjściowe (jakie wartości zwracamy)?

W tym przypadku danymi wejściowymi będą dwa punkty, które mogą być reprezentowane przez cztery parametry. Wartością, jaką będziemy zwracać, będzie właśnie odległość, będąca liczbą zmiennoprzecinkową.

Na początku możemy napisać szkielet funkcji, który odda obecny tok myślenia.

def distance(x1, y1, x2, y2):
    return 0.0

Oczywiście ta wersja funkcji nie obliczy żadnej odległości, zawsze zwróci zero. Jest ona jednak poprawna składniowo, uruchomiona zadziała co oznacza, że możemy ją przetestować zanim skomplikujemy ją nieco bardziej.

Aby przetestować nową funkcję, wywołamy ją z jakimiś prostymi wartościami.

def distance(x1, y1, x2, y2):
    return 0.0


print(distance(1, 2, 4, 6))

(ch06_distance1)

Wybraliśmy te właśnie wartości, by odległość w poziomie wynosiła 3, a w pionie 4, co pozwoli nam obliczyć odległość, wynoszącą 5 (przeciwprostokątną trójkąta o wymiarach 3-4-5). Testując działanie nowej funkcji, dobrze jest znać poprawną odpowiedź.

Sprawdziliśmy już, że funkcja jest poprawna składniowo, możemy zacząć dodawać nowe linie kodu. Po dopisaniu kolejnego kawałka będziemy ponownie testować funkcję. Jeżeli w jakimś punkcie programu pojawi się błąd, wiemy, gdzie on będzie - w linii, którą właśnie dodaliśmy.

Pierwszym logicznym krokiem w obliczeniach to znalezienie różnic x₂- x₁ oraz y₂- y₁. Te wartości będziemy przechowywać w tymczasowych zmiennych dx i dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    return 0.0

Teraz obliczymy sumę kwadratów zmiennych dx i dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx ** 2 + dy ** 2
    return 0.0

Moglibyśmy ponownie uruchomić program w obecnym stanie i sprawdzić wartość dsquared (powinna być równa 25).

Ostatecznie, używając połówkowego wykładnika 0.5 do obliczenia pierwiastka, liczymy i zwracamy wynik.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx ** 2 + dy ** 2
    result = dsquared ** 0.5
    return result


print(distance(1, 2, 4, 6))

(ch06_distancefinal)

Jeżeli funkcja działa poprawnie to by było na tyle. W innym przypadku można wydrukować wartość result przed wyrażeniem return.

Zaczynając, lepiej dodawać jedną, dwie linie kodu na raz. Gdy zyskacie nieco więcej wprawy prawdopodobnie będziecie pisać i debugować nieco większe części kodu. Rozwijając umiejętności programistyczne zaczniecie panować nad coraz większymi częściami kodu; jest to bardzo podobna procedura do nauki czytania – najpierw poznajemy litery, sylaby potem czytamy słowa, frazy, zdania i paragrafy.

Kluczowe zagadnienia tego procesu to:

Zaczynać z działającym szkieletem programu i dodawać niewielkie części kodu. Wtedy jeżeli znajdziecie błąd w dowolnym punkcie, to wiecie, gdzie on jest.
Używajcie zmiennych tymczasowych, aby przechowywać zmienne chwilowe, tak by w łatwy sposób można je było sprawdzić.
Jak już program działa, możecie połączyć kilka wyrażeń w jedno, nieco bardziej zwarte, ale tylko w przypadku, gdy nie powoduje to utraty czytelności programu.

Następna część - Składanie funkcji