Ćwiczenia¶

Użyj funkcji draw_square, którą zdefiniowaliśmy w tej części w programie, rysującym poniższy rysunek. Załóż, że każdy bok ma 20 jednostek. (Wskazówka: zauważ, że żółw odszedł od punktu końcowego ostatniego kwadratu w końcu programu.)
import turtle def draw_square(t, sz): """Uzyj zolwia t do narysowania kwadratu o boku sz""" for i in range(4): t.forward(sz) t.left(90) wn = turtle.Screen() wn.bgcolor("lightgreen") alex = turtle.Turtle() alex.color("pink") draw_square(alex,20) wn.exitonclick()

(ex_5_1)
import turtle def draw_square(t, sz): """Uzyj zolwia t do narysowania kwadratu o boku sz""" for i in range(4): t.forward(sz) t.left(90) wn = turtle.Screen() # Ustaw okno pracy i jego atrybuty wn.bgcolor("lightgreen") alex = turtle.Turtle() # stworz alexa alex.color('hotpink') alex.pensize(3) for i in range(5): draw_square(alex, 20) # Wywolaj funkcje rysujaca kwadrat alex.penup() alex.forward(40) # przesun alexa do pozycji poczatkowej by narysowac kolejny kwardat alex.pendown() wn.exitonclick()

(q1_answer)
Show Comments
Napisz program rysujący poniższy rysunek. Załóż, że najmniejszy wewnętrzny kwadrat ma bok o długości 20 jednostek, a kolejny, większy kwadrat ma bok większy o 20 jednostek od poprzedniego.
(ex_5_2)
Napisz funkcję nie zwracającą wartości draw_poly(zolw, boki, wielkosc) która za pomocą żółwia rysuje wielokąt regularny. Jeżeli wywołamy draw_poly(tess, 8, 50), to narysuje taki oto kształt:
(ex_5_3)
import turtle def draw_poly(t, num_sides, side_length): for i in range(num_sides): t.forward(side_length) t.left(360/num_sides) wn = turtle.Screen() wn.bgcolor("lightgreen") tess = turtle.Turtle() tess.color('hotpink') tess.pensize(3) draw_poly(tess, 8, 50)

(q3_answer)
Show Comments
Narysuj ten piękny wzorek.
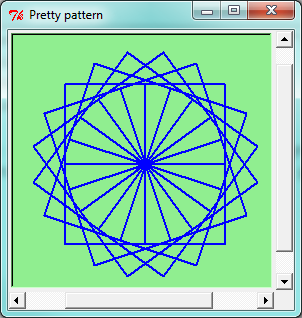
(ex_5_4)
Te spirale na rysunku poniżej różnią się tylko kątem obrotu. Narysuj obie.
(ex_5_5)
import turtle def draw_spiral(t, angle): ''' pobierz zolwia t do rysowania oraz kat w stopniach ''' length = 1 for i in range(84): t.forward(length) t.right(angle) length = length + 2 wn = turtle.Screen() wn.bgcolor("lightgreen") guido = turtle.Turtle() # stworz guido guido.color('blue') ## pierwsza spirala ## # ustaw guido guido.penup() guido.backward(110) guido.pendown() # narysuj spirale uzywajac obrotu o 90 stopnia draw_spiral(guido, 90) ## narysuj druga spirale ## # ustaw guido guido.home() guido.penup() guido.forward(90) guido.pendown() draw_spiral(guido, 89)

(q5_answer)
Show Comments
Napisz funkcję nie zwracającą wartości draw_equitriangle(someturtle, somesize), która bezpośrednio wywoła funkcję draw_poly z jednego z poprzednich zadań po to ,by narysować trójkąt równoboczny za pomocą żółwia.
(ex_5_6)
Napisz funkcję, zwracającą wartość sum_to(n), która oblicza sumę wszystkich liczb naturalnych mniejszych lub równych n. W takim przypadku wywołanie sum_to(n), będzie oznaczać 1+2+3+...+10, i powinniśmy dostać 55. Do obliczenia tej sumy użyj równania (n * (n + 1)) / 2.
from test import testEqual def sum_to(n): # tutaj kodujemy

(ex_5_7)
from test import testEqual def sum_to(n): result = (n * (n + 1)) / 2 return result # zobaczmy czy funkcja dziala t = sum_to(0) print("Suma od 1 do 0 wynosi", t) t = sum_to(10) print("Suma od 1 do 10 wynosi", t) t = sum_to(5) print("Suma od 1 do 5 wynosi", t)

(q7_answer)
Show Comments
Napisz funkcję area_of_circle(r), zwracającą pole koła o promieniu r. Upewnij się, że do rozwiązania użyjesz modułu math.
from test import testEqual def area_of_circle(r): # tutaj kodujemy t = area_of_circle(0) testEqual(t, 0) t = area_of_circle(1) testEqual(t, math.pi) t = area_of_circle(100) testEqual(t, 31415.926535897932)
(ex_5_8)
Napisz funkcję niezwracającą wartości, aby narysować gwiazdę pięcioramienną, której ramiona mają długość 100 jednostek.
(ex_5_9)
import turtle def draw_five_point_star(t): for i in range(5): t.forward(100) t.left(216) wolfram = turtle.Turtle() draw_five_point_star(wolfram)

(q9_answer)
Show Comments
Rozwiń powyższy program. Narysuj pięć gwiazd, ale pomiędzy każdą podnieś rysik, przenieś się do przodu o 350 jednostek, obróć o 144, opuść rysik i narysuj kolejną gwiazdę. Powinieneś dostać podobny rysunek (zauważ, że musisz przesunąć się w lewo rysując pierwszą gwiazdę, by zmieścić wszystko w jednym oknie):

Jak by wyglądał rysunek, gdybyście nie podnieśli rysika?
(ex_5_10)
Rozwiń funkcję rysującą gwiazdę, aby móc narysować gwiazdę n-ramienną. (Wskazówka: n musi być liczbą nieparzystą większą lub równą 3).
(ex_5_11)
import turtle def draw_star(t, n): for i in range(n): t.forward(100) t.left(180 - 180/n) stroustrup = turtle.Turtle() draw_star(stroustrup, 7)

(q11_answer)
Show Comments
Napisz funkcję draw_sprite, rysującą gąsiennicę. Funkcja będzie potrzebować parametrów, trzymających instancję żółwia, liczbę nóg oraz ich długość. Wywołaj tę funkcję, by narysowała gąsiennicę z 15 nogami o długości 120 jednostek.
(ex_5_12)
Przepisz funkcję sum_to(n) zwracającą sumę wszystkich liczb naturalnych do n włącznie. Tym razem użyj wzorca inkrementalnego.
def sum_to(n): # tutaj kodujemy

(ex_5_13)
def sum_to(n): sum = 0 for i in range(1,n+1): sum = sum + i return sum # zobaczmy czy funkcja dziala t = sum_to(0) print("Suma od 1 do 0 wynosi", t) t = sum_to(10) print("Suma od 1 do 10 wynosi", t) t = sum_to(5) print("Suma od 1 do 5 wynosi", t)

(q13_answer)
Show Comments
Napisz funkcję my_sqrt, która będzie przybliżała pierwiastek kwadratowy danej liczby n, używając algorytmu Newtona. Jest to algorytm iteracyjny, gdzie pierwsza rozwiązanie dane jest przez n/2, a każde kolejne obliczane jest ze wzoru newguess = (1/2) * (oldguess + (n/oldguess)).
(ex_5_14)
Skonstruuj funkcję my_pi, która zwróci przybliżenie liczby PI (3,1415…). Użyj przybliżenia Leibniza
(ex_5_15)
def my_pi(iters): ''' Obliczamy PI poprzez przybliżenie Leibnitza z liczbą iteracji równą iters ''' pi = 0 sign = 1 denominator = 1 for i in range(iters): pi = pi + (sign/denominator) sign = sign * -1 # zmienia znak z + na - denominator = denominator + 2 pi = pi * 4.0 return pi pi_approx = my_pi(10000) print(pi_approx)

(q15_answer)
Show Comments
Napisz funkcję my_pi, która obliczy przybliżoną wartość PI (3,1415…) za pomocą metody Madhava
(ex_5_16)
Zbuduj funkcję draw_fancy_square, która narysuje kwadrat z fantazyjnymi rogami (z kolcami w rogach). Użyj funkcji draw_sprite z zadania wcześniejszego. Aby dostać jeszcze ciekawszy wygląd można na końcach kolców dorysować małe trójkąty.
(ex_5_17)
import turtle def draw_sprite(t, numlegs, leglength): angle = 360/numlegs for i in range(numlegs): t.forward(leglength) t.backward(leglength) t.left(angle) def draw_fancy_square(t, sz, lgs, lgl): for i in range(4): t.forward(sz) drawSprite(t, lgs, lgl) t.left(90) wn = turtle.Screen() wn.bgcolor("lightgreen") alex = turtle.Turtle() draw_fancy_square(alex, 100, 10, 15) wn.exitonclick()

(q17_answer)
Show Comments

Następna część - Boolean Values and Boolean Expressions