Obliczanie przybliżenia wartości liczby PI¶
Niemal każdy słyszał o słynnej matematycznej liczbie zwanej Pi. Najczęściej jest ona używana do obliczania obwodu lub powierzchni koła. W przypadkach nie wymagających dużej dokładności używa się wartości Pi zaokrąglonej do 3.14. Matematycy ustalili, że liczba Pi należy do zbioru liczb niewymiernych, co oznacza, że posiada nieskończenie długie, nieokresowe rozwinięcie dziesiętne. Jej dokładniejsza wartość wynosi:
3.1415926535897932384626433832795028841971693993751058209749445923078164062…
W tym ćwiczeniu będziemy wyznaczać przybliżoną wartość liczby Pi, stosując metodę zwaną Symulacją Monte Carlo. Oznacza to, że wykorzystamy liczby losowe do symulacji doświadczenia losowego. Wynikiem serii takich doświadczeń będzie przybliżenie liczby Pi.
Podstawa symulacji¶
Gra, na której oprzemy symulację losową to „darts” („lotki”). Będziemy „losowo” rzucać dużą ilość lotek do odpowiednio przygotowanej tarczy. Wygląd tarczy pokazano na rysunku poniżej. Możemy zobaczyć, że w kwadratowy kawałek drewna wpisane jest koło o promieniu jednostkowym, a więc kwadratowa tarcza ma bok o długości 2.
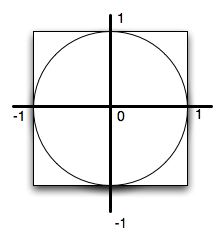
Ale jak to wszystko może być pomocne w wyznaczeniu przybliżonej wartość liczby Pi? Skupmy się na powierzchni okrągłej części tarczy. Jej promień wynosi 1, więc jej powierzchnia jest równa Pi. Drewniany kwadrat ma powierzchnię równą 4 (2x2). Iloraz powierzchni koła do powierzchni kwadratu jest równy Pi/4. Jeśli będziemy wykonywać dużą liczbę rzutów lotkami i będą one wbijały się w przypadkowe punkty na tarczy, to część z nich wbije się wewnątrz koła, a część na zewnątrz, na pozostałej powierzchni drewnianego kwadratu. Liczba lotek, które wbiły się wewnątrz koła podzielona przez liczbę wszystkich lotek wbitych w drewnianą tarczę będzie zbliżona do opisanego powyżej ilorazu powierzchni koła i kwadratu (Pi/4). Otrzymaną w ten sposób wartość wystarczy pomnożyć przez 4, aby otrzymać przybliżenie liczby Pi.
Lotkami ognia!¶
Po wymyśleniu metody symulacji możemy rozpocząć ostrzał tarczy lotkami. Załóżmy, że umiemy na tyle dobrze celować, że każda lotka po rzucie wbije się w drewniany kwadrat tarczy. Oczywiście część lotek wbije się wewnątrz koła na tarczy, a część poza nim.
Do symulacji rzutów lotkami można wygenerować 2 liczby losowe z przedziału pomiędzy zero i jeden. Pierwsza będzie oznaczała współrzędną „x” na tarczy, a druga współrzędną „y”. Jednakże, jak widać na rysunku, opisującym tarczę, możliwe współrzędne na tarczy są z przedziału od -1 do 1.
W jaki sposób przekształcić liczbę losową z przedziału od 0 do 1 na liczbę losową z przedziału od -1 do 1?
Poniżej w ramce wpisano szkic programu do realizacji opisanej symulacji. Uzupełnij część programu, która będzie odpowiedzialna za „rzucanie lotkami”. Do punktu trafienia na tarczy o współrzędnych x, y można po każdym rzucie przesunąć żółwia i postawić kropkę w tym punkcie (dot). Zwróć uwagę, że ogon żółwia jest w położeniu do góry, wiec żółw nie będzie rysował linii na tarczy.
(piguessstart)
Zliczanie lotek¶
Znana jest całkowita liczba rzuconych lotek. W zmiennej numdarts zapisano jej wartość. Potrzebujemy jeszcze liczbę lotek, które wbiły się wewnątrz koła. Ponieważ środek koła położony jest w punkcie o współrzędnych (0,0) i promień koła jest równy 1, zliczamy lotki, które wbiły się nie dalej niż w odległości 1 od środka. Szczęśliwie dysponujemy metodą żółwia o nazwie distance, która wyznacza odległość położenia żółwia od dowolnego innego punktu określonego parą liczb x, y.
Na przykład instrukcja fred.distance(12,5) wyznacza odległość położenia żółwia o „imieniu” fred od punktu (12,5).
Teraz wystarczy użyć powyższej metody w instrukcji warunkowej, aby sprawdzać, czy fred (przesunięty do miejsca trafienia lotki) jest w odległości mniejszej niż 1 od środka tarczy. Jeśli tak, zaznacz punkt trafienia lotki kolorem red (czerwonym), jeśli nie, kolorem blue (niebieskim). Jednocześnie, jeśli stwierdzimy, że punkt trafienia znajduje się wewnątrz koła, zliczamy to trafienie. W tym celu należy stworzyć zmienną w której będzie akumulowana liczba trafień w koło. Nazwij ją insideCount, zainicjuj ją wartością 0 i inkrementuj (powiększaj o 1), kiedy lotka trafi w koło. Pamiętaj, że w procesie inkrementacji wykorzystywana jest poprzednia wartość zmiennej insideCount.
Wyznaczenie wartości liczby Pi¶
Po zakończeniu wykonywania pętli w napisanym programie oraz narysowaniu miejsc trafień lotek musimy jeszcze obliczyć wartość Pi i wypisać ją. Użyj wzoru podanego wcześniej.
Uruchamiaj swój program, ustawiając coraz większe wartości zmiennej numdarts, aby uzyskać coraz dokładniejsze przybliżenie liczby Pi. Jeżeli chcesz przyspieszyć działanie programu dla dużych wartości zmiennej numdarts, ustaw tracer żółwia na wartość 100, stosując instrukcję fred.tracer(100).