Wykreślanie funkcji sinusoidalnej¶

Czym jest funkcja sinus?¶

Funkcja sinus, nazywana też sinusoidą, ma gładki kształt powtarzających się oscylacji, występujących w wielu dziedzinach nauki i techniki, w tym w matematyce, fizyce i zagadnieniach technicznych. Fragment funkcji sinus (jeden pełny okres) pokazano na wykresie poniżej. Zwróćcie uwagę, że oś x jest wyskalowana w stopniach.

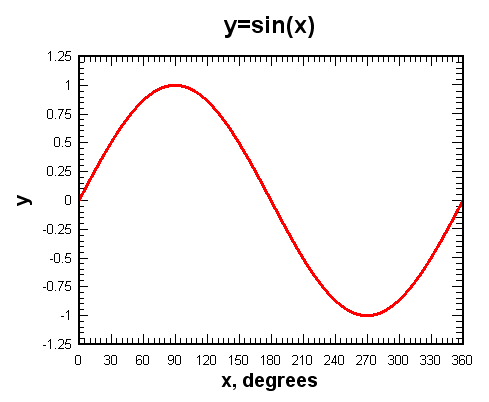
W tym ćwiczeniu zastosujemy bibliotekę math do wygenerowania wartości, których potrzebujemy. Pomocne w zrozumieniu funkcji sinus będzie rozważenie poniższego programu w języku Python. Jak widać, funkcja sin z biblioteki math ma tylko jeden argument (parametr). Wartość tego argumentu należy podawać w radianach (powinniście to pamiętać z zajęć z trygonometrii). Ponieważ jesteśmy w większości przyzwyczajeni do wyrażania kątów w stopniach, w bibliotece math zawarta jest funkcja radians do zamiany stopni na radiany.

Program pokazany powyżej pozwala obliczyć, że dla argumentu 90 stopni funkcja sinus przyjmuje wartość równą 1. Zauważmy że jest to zgodne z przedstawionym powyżej wykresem. Teraz spróbuj wpisać kilka innych wartości, jak 0o, 180o, 38o, i tak dalej. Otrzymane wyniki można porównać i dopasować do umieszczonego na początku rozdziału wykresu.

Ciekawsze od wpisywania pojedynczych wartości argumentu funkcji sinus będzie iteracyjne zadanie sekwencji kątów i obserwowanie, jak zmieniają się wartości funkcji. Spróbuj zadać kąty z zakresu od 0 do 180o. Co możesz powiedzieć o wynikach?

A teraz możesz spróbować to zrobić dla innych granicznych wartości kątów, jak na przykład 270 lub 360 stopni.

Tworzenie wykresu¶

W celu narysowania linii ciągłej na wykresie możemy zastosować metodę żółwia goto. Metoda goto ma dwa parametry, x i y, i przesuwa żółwia do położenia określonego przez te dwie współrzędne. Jeśli ogon żółwia jest skierowany w dół, zostanie narysowana linia od poprzedniego położenia do nowego położenia.

fred.goto(50,60)

Pamiętaj, że domyślnym położeniem żółwia jest pozycja w środku układu współrzędnych w punkcie (x=0, y=0). Możesz sobie wyobrazić obszar wykresu jako kartkę papieru milimetrowego. Oś x położona jest poziomo, a oś y pionowo. Osie przecinają się na środku kartki w punkcie (0, 0). Dla położeń na kartce, które leżą na lewo od środka wartość współrzędnej x jest ujemna. Dla położeń na kartce poniżej środka wartość współrzędnej y jest ujemna.

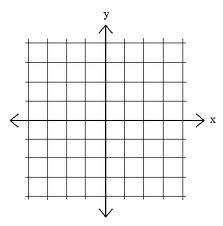
A teraz wypróbuj metodę goto. Poeksperymentuj, aż będziesz pewien, że system współrzędnych na ekranie jest dla Ciebie zrozumiały. Zastosuj zarówno dodatnie, jak i ujemne wartości współrzędnych punktów.

Teraz już możemy połączyć dwa poprzednie programy, aby ukończyć nasz wykres. Oto kolejne kroki:

1. Utwórz i ustaw żółwia na ekranie.

2. Zadawaj kolejne wartości kątów od 0 do 360 stopni.

   • Dla każdej wartości kąta wygeneruj, odpowiadającą mu wartość funkcji sinus.
   • Przesuń żółwia do położenia określonego przez te wartości (nie zamazując poprzednio narysowanych linii).

Poniżej przedstawiono szablon programu, który powinieneś uzupełnić.

Doskonalenie wykresu¶

Prawdopodobnie myślisz, że program ma błędy, ponieważ nie widać wykresu, jakiego się spodziewaliśmy. Czyżby wykres wyglądał jak linia prosta? Jak myślisz, na czym polega problem? Oto podpowiedź… zerknij powyżej i przyjrzyj się wartościom funkcji sinus obliczonym we wcześniejszym przykładzie.

Czy teraz widzisz, w czym tkwi problem? Wartości funkcji sinus leżą zawsze pomiędzy liczbami -1 i 1. Dla takiego zakresu wartości ruch żółwia po wykresie jest praktycznie niewidoczny.

W celu poprawy programu musimy inaczej zaprojektować „papier milimetrowy” na którym rysujemy przebieg funkcji sinus tak, aby zakres rysowanych wartości funkcji sinus wypełniał obszar wykresu. Aby to osiągnąć, należy zastosować metodę klasy Screen o nazwie setworldcoordinates. Metoda ta pozwala na zmiany zakresu wartości x i y w świecie żółwia. Zerknij do dokumentacji modułów żółwia w celu zapoznania się ze stosowaniem tej metody (Global Module Index – link). Kiedy już zrozumiesz sposób doboru parametrów metody, ustal właściwe parametry układu współrzędnych żółwia i na nowo uruchom program.