Klasyfikator kNN¶

Klasyfikator kNN (por. [Stapor2005], [Stapor2011]) to jedna z ważniejszych nieparametrycznych metod klasyfikacji. W tej metodzie klasyfikowany obiekt przydzielamy do tej klasy, do której należy większość z jego:math:k sąsiadów. Załóżmy, że w sposób niezależny wylosowano \(n\) obiektów \(x_1,\ldots,x_n\) z populacji o rozkładzie \(f(x)\). Prawdopodobieństwo, że \(k\) spośród tych obiektów znajduje się w pewnym obszarze \(R\) można estymować za pomocą średniej frakcji obiektów, które są w obszarze \(R\) (por. [Duda2000]) tzn

\[P\cong\frac{k}{n}\]

Jeśli dodatkowo założymy, że obszar \(R\) jest na tyle mały, że funkcja gęstości jest w nim stała, to wówczas otrzymujemy

\[f(x)\cong\frac{k}{nv}\]

gdzie \(v\) jest objętością obszaru \(R\). Uzyskaliśmy w ten sposób ogólny wzór określający estymator funkcji gęstości \(f(x)\) w punkcie \(x\) przestrzeni cech. Estymator warunkowej gęstości w \(j\)-tej klasie dany jest wzorem

\[f(x|j)=\frac{k_j}{n_jv}\]

gdzie \(n_i\) to liczba wszystkich obiektów z klasy \(j\) w zbiorze uczącym, \(k_j\) jest liczbą obiektów z \(j\)-tej klasy, które znalazły się pośród \(k\) najbliższych sąsiadów obiektu \(x\). Ponadto zachodzi równość

\[k=\sum_{j\in I} k_j\]

Korzystając ze wzoru Bayesa uzyskujemy oszacowanie prawdopodobieństwa a posteriori \(j\)-tej klasy w punkcie \(x\) dane wzorem

\[P(j|x)=\frac{f(x|j)p(j)}{\sum_{j=1,\ldots,L}f(x|j)p(j)}=\frac{\frac{k_j}{n_jv}\frac{n_j}{n}}{\sum_{j=1,\ldots,L}\left(\frac{k_j}{n_jv}\frac{n_j}{n}\right)}=\frac{k_j}{k}\]

stąd otrzymujemy, że funkcje dyskryminacyjne klasyfikatora kNN są postaci

\[g_j(x)=\frac{k_j}{k}\]

gdzie \(k_j\) oznacza liczbę wektorów zbioru uczącego z \(j\)-tej klasy, które znajdują się pośród \(k\) najbliższych sąsiadów obiektu \(x\). Reguła decyzyjna klasyfikator kNN jest następująca

\[\begin{split}\phi_{kNN}(x)=i\Leftrightarrow\forall_{j=1,\ldots, L, j\neq i} \quad g_i(x)>g_j(x)\end{split}\]

Zatem klasyfikator kNN zalicza klasyfikowany obiekt do tej klasy, która jest najliczniej reprezentowana wśród \(k\) najbliższych sąsiadów ze zbioru uczącego. Ponadto klasyfikator kNN wymaga ustalenia liczby \(k\). Jednym ze sposobów wyboru liczby \(k\) jest uzależnienie liczby \(k\) od liczby obiektów w zbiorze uczącym w takim sposób by zachodziły poniższe warunki

\[\begin{split}\lim_{n\to\infty}k(n)=\infty\\ \lim_{n\to\infty}k(n)/n=0\end{split}\]

Wówczas estymator typu najbliższy sąsiad będzie estymatorem zgodnym. Powyższe warunki spełnia

\[k(n)=c\sqrt{n}\]

gdzie \(c>0\) jest pewną stałą. Innym sposobem ustalenia wartości liczby \(k\) jest jej dobór w trakcie walidacji na przykład metodą k-krotnej walidacji krzyżowej.

Algorytm 2 Klasyfikator kNN

Dane: zbiór uczący \(X_{train}=\{(x_i,y_i):x_i\in X, y_i\in C=\{-1,1\}\}\), \(x\) - klasyfikowany obiekt, \(k\) - liczba sąsiadów, \(N\) - liczebność zbioru uczącego

Wyniki: \(y\in\{1,2\}\) - etykieta klasy

\(\mathbf{for} \ j=1 \ \mathbf{to} \ N \ \mathbf{do}\)

\(\qquad d_j=\|x-x_j\|\)

Posortuj odległości \(d_j\) od najmniejszej do największej

Wybierz \(k\) najbliższych sąsiadów

Przypisz obiekt do klasy liczniej reprezentowanej

Przykład 5

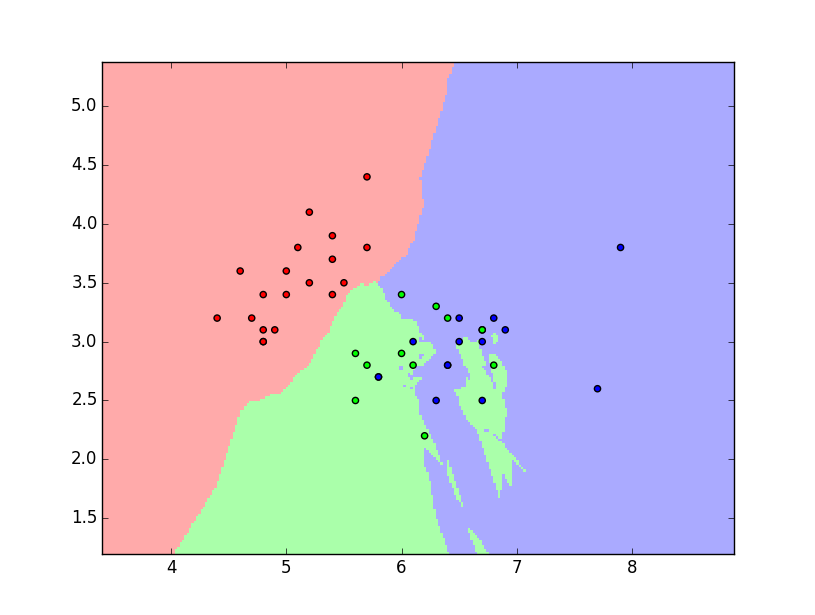
Ponownie rozważmy zbiór danych iris. W tym przykładzie ograniczamy liczbę cech obiektów do 2. Zbiór iris dzielimy, w sposób losowy na dwie części: uczącą i testową w stosunku 70:30. Następnie przeprowadzamy na zbiorze uczącym proces uczenia klasyfikatora kNN dla parametru \(k=9\). Na płaszczyźnie 2D zaznaczamy obszary decyzyjne i obiekty zbioru testowego. Dla wybranego parametru \(k\) klasyfikator kNN osiągnął sprawność \(80\%\). Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę oraz wykres przedstawiający obszary decyzyjne wraz z obiektami (rys 1).

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
from sklearn.cross_validation import train_test_split

k = 9

#importujemy zbiór danych
iris = datasets.load_iris()

#Zbiór obiektów
X = iris.data[:, :2]
# W niniejszym przykładzie interesują nas jedynie pierwsze
#dwie cechy obiektów

#Wektor poprawnej klasyfikacji obiektów
y = iris.target

#Dzielimy losowo zbiór na dwie części
train, test, train_targets, test_targets = train_test_split(X, y,
                                 test_size=0.30, random_state=42)

h = .02

#Tworzymy kolorową mapę
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])

#Tworzymy klasyfikator.
#Jako metrykę przyjmujemy metrykę euklidesową.
clf = neighbors.KNeighborsClassifier(k, weights='uniform',
                                     metric='euclidean')

#Uczymy klasyfikator
clf.fit(train, train_targets)

#Ustalamy wielkość wykresu
#Dla każdego obszaru decyzyjnego przypisany zostanie inny kolor
x_min, x_max = test[:, 0].min() - 1, test[:, 0].max() + 1
y_min, y_max = test[:, 1].min() - 1, test[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

#Testujemy klasyfikator
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

#Sprawdzamy sprawność klasyfikatora
print "Sprawność klasyfikatora: %f" % clf.score(test,test_targets)

#Umieszczamy wyniki na rysunku
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)

#Umieszczamy elementy zbioru testowego na rysunku
plt.scatter(test[:, 0], test[:, 1], c=test_targets, cmap=cmap_bold)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

Następna część - Liniowe metody klasyfikacji