Liniowy klasyfikator SVM¶

Rozważmy zadanie klasyfkiacji dla dwóch klas, oznaczonych etykietami -1 oraz 1, zatem niech dany będzie zbiór uczący postaci:

\[{{X}_{train}}=\left\{ \left( {{x}_{1}},{{y}_{1}} \right),...,\left( {{x}_{N}},{{y}_{N}} \right)\in {{R}^{p}}\times \left\{ -1,+1 \right\} \right\}\]

Regułę decyzyją \(g\) klasyfikatora określamy w ten sposób, że obiekt jest zaliczany do klasy 1, gdy \(g(x)\ge 0\), a do klasy -1, gdy \(g(x)< 0\). Uczenie klasyfikatora liniowego polega na znalezieniu hiperpłaszczyzny rozdzielającej o równaniu:

\[{{w}^{T}}x+w_0=0,\]

gdzie \(x\) jest klasyfikowanym wektorem, \(w\) -wektorem wag, \(b\) -przesunięcie (bias).

Przypadek liniowo separowalny¶

Rozważanie przypadku liniowo separowalnego gwarantuje istnienie hiperpłaszczyzny poprawnie rozdzielającej wszystkie próbki zbioru uczącego. Wśród nieskończenie wielu rozwiązań za optymalną w sensie SVM uważamy hiperpłaszczyznę rozdzielającą maksymalizującą tak zwany margines. Pojęcie marginesu i optymalnej hiperpłaszczyzny rozdzielającej definiujemy poniżej:

Definicja 19

Marginesem hiperpłaszczyzny rozdzielającej nazywamy odległość tej hiperpłaszczyzny od najbliższego wektora cech próbki w zbiorze uczącym.

Prawdziwe jest następujące twierdzenie:

Twierdzenie 4

Niech \(g(x)=w^Tx+w_0\) będzie funkcją dyskryminującą, gdzie \(w\) oraz \(b\) są odpowiednio wektorem wag oraz przesunięciem dla hiperpłaszczyzny rozdzielającej. Wtedy odległość wektora cech \(x\) od tej hiperpłaszczyzny rozdzielającej wynosi

\[r=\frac{g(x)}{\|w\|},\]

Definicja 20

Optymalną hiperpłaszczyzną rozdzielającą OSH (ang. Optimal Separating Hyperplane) nazywamy hiperpłaszczyznę rozdzielającą charakteryzującą się maksymalnym marginesem.

Definicja 21

Wektorami podpierającymi SV (ang. Support Vector) nazywamy wektory zbioru uczącego położone najbliżej optymalnej hiperpłaszczyzny rozdzielającej, czyli takie, dla których spełniony jest warunek

\[\begin{split}\alpha_i>0\end{split}\]

gdzie \(\alpha=[\alpha_1,\ldots,\alpha_{n_{train}}]\) są mnożnikami Lagrange’a, lub równoważnie

\[y_i\left(w^Tx_i+w_0\right)-1=0.\]

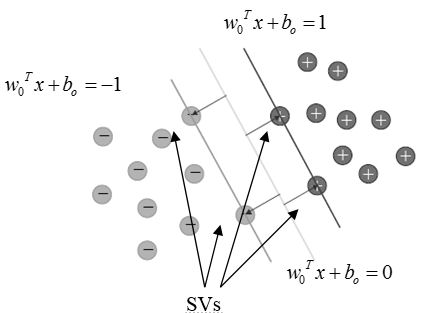
Położenie optymalnej hiperpłaszczyzny rozdzielającej, oraz umiejscowienie wektorów podpierających ilustruje rysunek 1

Rysunek 1: Wektory podpierające.

Zauważmy, że zbiór rozwiązań będący hiperpłaszczyznami optymalnymi również jest nieskończony, bowiem każde przeskalowanie wartości wektora wag \(w\) i przesunięcia \(b\) OSH nadal stanowi rozwiązanie optymalne. Spośród wszystkich hiperpłaszczyzn będących OSH wybieramy tzw kanoniczną optymalną hiperpłaszczyznę rozdzielającą.

Definicja 22

Kanoniczną optymalną hiperpłaszczyzną rozdzielającą nazywamy taką hiperpłaszczyznę, dla której moduł wartości funkcji dyskryminacyjnej dla próbki uczącej połóżonej najbliżej niej jest równy 1, czyli

(1)\[|w^Tx+w_0|=1.\]

Z faktu, że spośród optymalnych hiperpłaszczyzn rozdzielających wybieramy kanoniczną hiperpłaszczyznę rozdzielającą, czyli spełniającą warunek (1) wynika na mocy twierdzenia 4 wynika, że dla każdej próbki ze zbioru uczącego \((x_i,y_i)\in X_{train}\times \{-1,1\}\) zachodzi następujący warunek:

\[y_i(w^Tx_i+w_0)\geq 1.\]

Przypomnijmy, że celem uczenia liniowego klasyfikatora SVM jest maksymalizacja marginesu co na podstawie powyższego równoważne jest minimalizacji normy kwadratowej wektora \(w\). Proces uczenia sprowadza się zatem do wyznaczenia wartości wektora wag \(w\) i przesunięcia \(w_0\) tak aby zminimalizować następującą funkcję kryterialną:

(2)\[J(w,w_0)=\frac{1}{2}\|w\|^2\]

przy warunkach

(3)\[y_i(w^tx_i+w_0)\geq 1 \quad\textrm{ dla } i=1,\ldots,N,\]

gdzie \(N\) jest liczebnością próbek zbioru uczącego. Powyższe zadanie stanowi problem optymalizacji kwadratowej wypukłej funkcji kosztu \((p+1)\) zmiennych z \(N\) ograniczeniami liniowymi.

Wykorzystując metodę mnożników Lagrange’a, można sformułować zadanie pierwotne dla zadania optymalizacji funkcji kryterialnej (2) z warunkami (3) otrzymujemy zadanie optymalizacji funkcji Lagrange’a postaci:

(4)\[L(w,w_0,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^{N}\alpha_i\left[y_i\left(w^tx_i+w_0\right)-1\right]\!,\]

gdzie \(\alpha=[\alpha_1,\ldots,\alpha_{N}]\) są mnożnikami Lagrange’a stowarzyszonymi z odpowiednimi ograniczeniami. Funkcję Dla tak zdefiniowanego zadania pierwotnego należy dokonać minimalizacji funkcji \(L\) ze względu na \(w\) i \(w_0\), oraz maksymalizacji względem \(\alpha_i\). Rozwiązaniem zadania (4) jest punkt siodłowy funkcji \(L(w,w_0,\alpha)\). Problem optymalizacyjny rozwiązać można poprzez sprowadzenie go do rozwiązania zadania dualnego jako zadania maksymalizacji funkcji \(L\) przy spełnieniu warunków zerowania się pochodnych cząstkowych funkcji Lagrange’a, i przez zapewnienie nieujemności wszystkich współczynników Lagrange’a, a zatem:

\[\begin{split}\frac{\partial L(w,w_0,\alpha)}{\partial w}=0\label{L1},\\ \frac{\partial L(w,w_0,\alpha)}{\partial w_0}=0,\end{split}\]

\[\alpha_i\geq 0.\]

Obliczając powyższe pochodne cząstkowe mamy:

\[\frac{\partial L\left( w,{{w}_{0}},\alpha \right)}{\partial w}=\frac{1}{2}\cdot 2w-\frac{\partial \sum\limits_{i=1}^{N}{\left[ {{\alpha }_{i}}{{y}_{i}}{{w}^{T}}{{x}_{i}}+{{\alpha }_{i}}{{y}_{i}}{{w}_{0}}-{{\alpha }_{i}} \right]}}{\partial w}=w-\sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{y}_{i}}{{x}_{i}}}=0\]

\[\frac{\partial L\left( w,{{w}_{0}},\alpha \right)}{\partial {{w}_{0}}}=0-\sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{y}_{i}}}=0\]

czyli:

(5)\[w=\sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{y}_{i}}{{x}_{i}}}\]

(6)\[\sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{y}_{i}}}=0\]

Wstawiając powyższe do (4) uzyskujemy następującą postać zadania dualnego dla rozważanego problemu optymalizacyjnego:

(7)\[Q(\alpha)=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_iy_jx_i^Tx_j,\]

którego rozwiązanie optymalne poszukujemy w zależności od \(\alpha=[\alpha_1,\ldots,\alpha_{N}]\) przy ograniczeniach:

\[\begin{split}\alpha_i\geq 0,\\ \sum_{i=1}^{N}\alpha_iy_i=0.\end{split}\]

Ponieważ zadanie wyznaczenia optymalnej hiperpłaszczyzny rozdzielającej jest zadaniem optymalizacji kwadratowej z wypukłą funkcją kosztu, zatem można dla niego podać warunki Kuhna - Tuckera [Luenberger1974], które są warunkami koniecznymi i wystarczającymi istnienia minimum funkcji celu. Dla zadania wyznaczenia optymalnej hiperpłaszczyzny rozdzielającej OSH warunki te mają postać:

(8)\[\alpha_i\left[y_i\left(w^Tx_i+w_0\right)-1\right]=0.\]

dla \(i=1,...,N\)

Po wyznaczeniu optymalnych wartości \(\alpha_i\), wartość wektora wag \(w\) optymalnej hiperpłaszczyzny rozdzielającej obliczamy zgodnie ze wzorem (5) natomiast wartość przesunięcia zgodnie ze wzorem:

\[{{w}_{0}}=1-w^{T}{{x}^{\left( s \right)}},\]

gdzie \(x^{(s)}\) jest wektorem podpierającym.

Na podstawie optymalnego zestawu mnożników Lagrange’a wektory podpierające są bardzo łatwe do zidentyfikowania, bowiem jedynie im odpowidające mnożniki Lagrange’a są nie zerowe a dokładniej większe od zera. Zauważmy więc, że wektory podpierające są jedynymi wektorami zbioru uczącego, które mają wpływ na położenie hiperpłaszczyzny rozdzielającej.

Przykład 13

W tym przykładzie prezentujemy działanie liniowego klasyfikatora SVM dla przypadku liniowo separowalnego. Pakiet scikit-learn nie wymaga oznaczania klas etykietami -1 oraz 1. W przykładzie przyjmujemy oznaczenia 0 oraz 1. Na początku generujemy losowo zbiór danych uczących i testowych. Rozkłady cech w klasach są dwuwymiarowymi rozkładami normalnymi z odpowiednimi parametrami. Prezentujemy wykres próbek uczących w przestrzeni cech aby zauważyć, że faktycznie mamy do czynienia z przypadkiem liniowo separowalnym. W dalszej części dokonujemy uczenia klasyfikatora, odczytujemy współrzędne i liczbę wektorów podpierających. Na wykresie zaznaczamy te wektory oraz optymalną hiperpłaszczyznę rozdzielającą, w końcowym etapie dokonujemy testowania na niezależnym od zbioru uczącego zestawie danych testowych.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC


#generujemy dane dla problemu liniowo separowalnego
class1=np.random.multivariate_normal([1,3],[[1,0.7],[0.7,0.9]],20)
class2=np.random.multivariate_normal([6,2],[[0.6,0],[0,0.8]],20)
TrainData=np.vstack([class1[0:10,:],class2[0:10,:]])
TestData=np.vstack([class1[10:20,:],class2[10:20,:]])
TrainClasses=[0]*10+[1]*10
TestClasses=TrainClasses

#wykres ilustrujący zbiór uczący w przestrzeni cech
plt.scatter(TrainData[0:10,0],TrainData[0:10,1],c='b')
plt.scatter(TrainData[10:20,0],TrainData[10:20,1],c='r')
plt.show()

#Parametry liniowego klasyfikatora SVM
svm = SVC(kernel="linear", C=100)

#Uczenie klasyfikatora
svm.fit(TrainData,TrainClasses)

#Obiekt nauczonego klasyfikatora przechowuje takie informacje jak:
print 'Numery próbek będące wektorami podpierającymi'
print svm.support_
print 'Wektory zbioru uczącego będące wektorami podpierającymi'
print svm.support_vectors_
print 'Liczba wektrów podpierających w poszczególnych klasach'
print svm.n_support_


#Optymalna hiperpłaszczyzna rozdzialająca
w = svm.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-1, 7)
yy = a * xx - (svm.intercept_[0]) / w[1]

#Wyznaczamy proste równoległe do OSH odległe od niej o wartość marginesu
#Na prostych tych znajdują się wektory podpierające
b = svm.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = svm.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])

#Narysowanie OSH i prostych równoległych
plt.plot(xx, yy, 'k-')
plt.plot(xx, yy_down, 'k--')
plt.plot(xx, yy_up, 'k--')
#Zaznaczenie na wykresie wektorów podpierających
plt.scatter(svm.support_vectors_[:, 0], svm.support_vectors_[:, 1],
            s=80, facecolors='none')
plt.scatter(TrainData[:, 0], TrainData[:, 1], c=TrainClasses, cmap=plt.cm.Paired)

plt.axis('tight')
plt.show()

#Testowanie klasyfikatora na zbiorze uczącym
y = svm.predict(TestData)
print 'Etykiety klas dla zbioru testowego'
print y

#Sprawność klasyfikatora na zbiorze testowym
print 'Sprawność klasyfikatora:'
print svm.score(TestData,TestClasses)

Przypadek liniowo nieseparowalny¶

Rozważmy teraz przypadek liniowo nieseparowalny. Sytuacja taka oznacza, że nie istnieje hiperpłaszczyzna rozdzielająca zapewniająca poprawną klasyfikację wszystkich elementów zbioru uczącego. Pewne wektory zbioru uczącego położone będą zatem po nieodpowiedniej stronie hiperpłaszczyzny rozdzielającej. W takim przypadku poszukujemy hiperpłaszczyzny, która minimalizuje prawdopodobieństwo błędnej klasyfikacji poprzez wprowadzenie tak zwanego miękkiego marginesu.

Jeżeli próbka \((x_i,y_i)\) narusza warunek \({{y}_{i}}\left( {{w}^{T}}{{x}_{i}}+{{w}_{0}} \right)\ge 1\) może dziać się tak w dwóch przypadkach:

Próbka wpada w obszar separacji ale jest po odpowiedniej stronie hiperpłaszczyzny decyzyjnej (zapewniającej poprawną klasyfikację).
Próbka jest po przeciwnej stronie hiperpłaszczyzny decyzyjnej co oznacza, że zostanie niepoprawnie zaklasyfikowana.

Dla każdego obiektu zbioru uczącego \(x_i\in X_{train}\) wprowadza się tak zwane zmienne osłabiające \(\xi_i\) otrzymując wspomniany miękki margines. Pojęcie zmiennej osłabiającej definiujemy formalnie poniżej.

Definicja 23

Zmienną osłabiająca dla wektora \(x_i\) zbioru uczącego \(X_{train}\) nazywamy minimalną wartość \(\xi_i\ge 0\) odchylenia wektora \(x_i\) od przypadku liniowej separowalności taką, że

(9)\[y_i(wx_i+w_0)\geq 1-\xi_i \textrm{ dla } i=1,\ldots,N.\]

Wartości \(\xi_i\in[0,1]\) oznaczają, że wektor \(x_i\) zbioru uczącego \(X_{train}\) znajduje się w obrębie marginesu po właściwej stronie optymalnej hiperpłaszczyzny rozdzielającej, natomiast wartości \(\xi_i>1\) oznaczają, że wektor \(x_i\) zbioru uczącego znajduje się po niewłaściwej stronie hiperpłaszczyzny rozdzielającej.

Wprowadzenie zestawu zmiennych osłabiających determinuje poniższą modyfikację funkcji celu, która w tym przypadku przyjmuje następującą postać

(10)\[J(w,w_0)=\frac{1}{2}\|w\|^2+C\sum_{i=1}^{N}\xi_i,\]

gdzie parametr \(c\) jest parametrem regularyzacyjnym i stanowi kompromis pomiędzy złożonością klasyfikatora a liczbą błędnych decyzji.

Zadanie uczenia klasyfikatora w przypadku liniowo nieseparowalnym sprowadza się do optymalizacji funkcji celu (10) przy warunkach (9). Postępując analogicznie jak poprzednio możemy sprowadzić powyższe zadanie do postaci dualnej, która polega na wyznaczeniu mnożników Lagrange’a na podstawie wektorów zbioru uczącego \(X_{train}\), tak aby zmaksymalizować funkcję

(11)\[Q(\alpha)=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_iy_jx_i^Tx_j\]

względem \(\alpha=\begin{array}{lll}\left[\alpha_1,\ldots, \alpha_{n_{train}}\right]\end{array}\) przy ograniczeniach

\[\sum_{i=1}^{N}\alpha_iy_i=0,\quad 0\leq\alpha_i\leq C.\]

Rozwiązanie dla wektora wag \(w\), podobnie jak poprzednio jest dane wzorem (5). Wartość obciążenia \(w_0\) uzyskujemy natomiast w oparciu o wzór (6) wybierając wektor podpierający, dla którego \(\xi_i=0\)

Schemat działania liniowej maszyny wektorów podpierających przedstawia algorytm 12.

Algorytm 13 Algorytm SVM

Dane: zbiór uczący \((x_i,y_i)\in X_{train}\times \{-1,1\}\)

Wyniki: Wektor wag \(w\) oraz przesunięcie \(w_0\) optymalnej hiperpłaszczyzny rozdzielającej OSH

Wyznacz współczynniki Lagrange’a na podstawie wektorów zbioru uczącego \(X_{train}\) rozwiązując problem maksymalizacji funkcji kosztu danej poniższym wzorem:

\[Q(\alpha)=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_iy_jx_i^Tx_j\]

względem \(\alpha=[\alpha_1,\ldots, \alpha_{N}]\) przy ograniczeniach postaci:

\[\sum_{i=1}^{N}\alpha_iy_i=0,\quad 0\leq\alpha_i\leq C.\]
Na powstawie uzyskanych mnożników Lagrange’a oblicz wektor wag \(w\) optymalnej hiperpłaszczyzny rozdzielającej OSH zgodnie ze wzorem:

\[w=\sum_{i=1}^{N}\alpha_iy_ix_i.\]
Oblicz wartość przesunięcia \(w_0\) wybierając wektor podpierający, dla którego \(\xi_i=0\) za pomocą poniższego wyrażenia:

\[\alpha_i\left[y_i\left(w^Tx_i+w_0\right)-1+\xi_i\right]=0.\]

Przykład 14

W tym przykładzie prezentujemy działanie liniowego klasyfikatora SVM dla przypadku liniowo nieseparowalnego. Na początku generujemy za pomocą pakietu scikit-learn zbiór danych uczących w kształcie odwróconych zachodzących na siebie księżyców. Na zaprezentowanym wykresie próbek uczących w przestrzeni zauważamy, że rozważany przypadek jest liniowo nieseparowalny. W dalszej części dokonujemy uczenia klasyfikatora i oceny jego sprawności na zbiorze testowym. W tym przypadku oczywiście uzyskanie bezbłędnej klasyfikacji wszystkich elementów zbioru testowego jest niemożliwe. Na wykresie zaznaczamy powierzchnie rozdzielającą uzyskanego klasyfikatora oraz obszary decyzyjne.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_moons
from sklearn.cross_validation import train_test_split


#generujemy dane w kształcie odwróconych księżyców
Data,Classes = make_moons(noise=0.2)

#Podział na część uczącą i testową
TrainData, TestData, TrainClasses, TestClasses = train_test_split(Data, Classes, test_size=.5)

#Parametry klasyfikatora SVM
svm=SVC(kernel="linear", C=0.1)

#wartość kroku
h=0.025
x_min, x_max = Data[:, 0].min() - .5, Data[:, 0].max() + .5
y_min, y_max = Data[:, 1].min() - .5, Data[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
#dane uczące
plt.scatter(TrainData[:, 0], TrainData[:, 1], c=TrainClasses, cmap=cm_bright)
#dane testowe
plt.scatter(TestData[:, 0], TestData[:, 1], c=TestClasses, cmap=cm_bright, alpha=0.6)
#wyświetlenie wykresu
plt.show()

#uczenie klasyfikatora
svm.fit(TrainData,TrainClasses)
#uzyskana sprawnosc
score = svm.score(TestData, TestClasses)
print 'Sprawność na zbiorze testowym'
print score

#Generujemy wykres powierzchni rozdzielającej
Z = svm.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=cm_bright, alpha=.8)
#Wyświetlenie elementów zbioru uczącego
plt.scatter(TrainData[:, 0], TrainData[:, 1], c=TrainClasses, cmap=cm_bright)
#Wyświetlenie elementów zbioru testowego
plt.scatter(TestData[:, 0], TestData[:, 1], c=TestClasses, cmap=cm_bright,alpha=0.6)
plt.show()

Następna część - Nieliniowy klasyfikator SVM