Zmniejszanie wymiarowości przestrzeni poprzez ekstrakcję cech¶

Liniowa Analiza Dyskryminacyjna¶

Metoda Liniowej Analizy Dyskryminacyjnej (LDA) (ang. Linear Discriminant Analysis) (por. [Hestie2001], [Fukunaga1990], [Duda2000], [Marques2001]) jest najstarszym podejściem do redukcji przestrzeni wymiaru cech. Podejście to zostało zaproponowane w 1936r. przez sir Rolanda Fishera [Fisher1936]. W metodzie tej zakładamy, że wektory obserwacji są wektorami z \(p\)-wymiarowej przestrzeni euklidesowej. Metoda LDA prowadzi do otrzymania reguły decyzyjnej opartej na funkcji liniowej. Autor metody rozważał jedynie przypadek z dwiema klasami, jednak jego rozwiązanie możemy uogólnić na przypadek większej liczby klas. Uogólnienie to przedstawimy w następnym podrozdziale, natomiast teraz rozważmy problem dwuklasowy.

Załóżmy, że mamy \(n\) próbek o znanej przynależności do klas, z czego \(n_1\) próbek należy do klasy \(C_1\), natomiast \(n_2\) próbek należy do klasy \(C_2\). Oczywiście \(n_1+n_2=n\). Niech zatem \(x_1,\ldots,x_n\) będą naszymi próbkami w \(p\)-wymiarowej przestrzeni cech \(X\).

Oznaczmy przez \(y_i\)

liniową kombinację cech \(x_i\). Występujący w powyższym równaniu \(p\) wymiarowy wektor \(w\) możemy traktować jako linię w \(p\) wymiarowej przestrzeni cech, natomiast \(y_i\) jako projekcję wektora \(x_i\) na tą prostą.

Ponadto niech

będzie pewną funkcją liniową. Załóżmy, że wartość funkcji \(h(x_i)>0\) jeśli element \(x_i\) należy do klasy \(C_1\), w przeciwnym wypadku obiekt \(h(x_i)<0\). Naszym celem jest znalezienie optymalnych współczynników \(w\) oraz progu \(w_0\). Zmienna

w rzutowanej jednowymiarowej przestrzeni jest klasyfikowana do jednej z klas w zależności od wartości. Jeśli \(y<-w_0\) to zmienna \(y\) zostanie zaklasyfikowana do klasy \(C_1\), natomiast jeśli \(y>w_0\) to \(y\in C_2\).

Ponadto jeśli zmienna \(x_i\) ma rozkład normalny, to \(h(x_i)\) także ma rozkład normalny oraz zachodzą warunki

gdzie funkcje \(\eta_i\) oraz \(\sigma_i^2\) są kryteriami miary separowalności klas w rzutowanej przestrzeni. Jeśli natomiast \(x_i\) nie ma rozkładu normalnego, wówczas z twierdzeń granicznych wynika, że \(h(x_i)\) nadal może mieć rozkład normalny dla wystarczająco dużego \(p\). Wartość oczekiwana \(h(x_i)\) wyraża się następującym wzorem

gdzie \(M_i\) jest wektorem wartości średnich w klasie \(C_i\). Wariancja \(h(x_i)\) jest postaci

gdzie \(S_i\) jest próbkową macierzą kowariancji dla klasy \(C_i\) daną wzorem

Oznaczmy przez \(J(\eta_1,\eta_2,\sigma_1^2,\sigma_2^2)\) funkcję kryterialną optymalizowaną w celu obliczenia wartości \(w\) oraz \(w_0\). Korzystając z twierdzenia o pochodnej funkcji złożonej, otrzymujemy

oraz

Ponadto,

Dokonując odpowiednich podstawień w (1) i (2) dostajemy

i

Przyrównując obydwie powyższe pochodne do zera otrzymujemy

oraz

Błąd w rzutowanej przestrzeni zależy tylko od kierunku wektora \(w\) a nie od jego długości. Dlatego też dla uproszczenia możemy usunąć wszystkie stałe, przez które mnożymy wektor \(w\). Stąd mamy wzór na postać optymalnych współczynników wektora \(w\)

gdzie

W zależności od wyboru funkcji \(J\) otrzymujemy różne postacie algorytmu Liniowej Analizy Dyskryminacyjnej. Jedną z możliwych postaci funkcji \(J\) jest funkcja kryterialna Fishera. Sprowadza ona algorytm LDA do algorytmu Liniowej Dyskryminacji Fishera (ang. Fisher Linear Discriminat) FLD.

Liniowa Dyskryminacja Fishera¶

Rozważmy funkcję kryterialną Fishera daną wzorem

Istotą liniowej dyskryminacji Fishera (ang. Fisher Linear Discriminant (FLD)) (por. [Hestie2001], [Fukunaga1990], [Duda2000], [Marques2001]) jest znalezienie takiej prostej \(w\), aby po rzutowaniu wektorów wejściowych na tą prostą uzyskać najlepsze rozdzielenie wektorów z klasy \(C_1\) oraz \(C_2\). Miarą rozdzielności klas przyjętą przez Fishera jest funkcja kryterialna (5). Istnieją różne metody pozwalające wyznaczyć wektor \(w\) maksymalizujący kryterium (5). Zgodnie z metodą opisaną w [Schalkoff1992] w tym celu wystarczy obliczyć pochodne funkcji \(J\) względem \(\sigma_1^2\) oraz \(\sigma_2^2\). Są one następującej postaci

Stąd dzięki (3) i (4) dla funkcji \(J\) postaci (5) dostajemy

oraz

Ponieważ w różnicy \(\eta_2-\eta_1\) nie występuje czynnik \(w_0\), kryterium Fishera nie zależy od progu \(w_0\). Czynnik ten zmienia jedynie długość wektora, który wyznacza kierunek prostej. Mając dany wektor \(w\) możemy dokonać klasyfikacji. Wówczas klasyfikowany wektor \(x_i\) oraz wektory wartości średnich w obu klasach rzutujemy na prostą wyznaczoną przez wektor \(w\). Następnie wyznaczamy odległości pomiędzy rzutem wektora \(x_i\) na prostą \(w\) oraz rzutami wartości średnich na tą prostą. Klasyfikowany wektor \(x_i\) przypisujemy do klasy, dla której obliczona odległość będzie mniejsza. Poniżej przedstawiamy schemat algorytmu FLD.

Rysunek 1 ilustruje prostą dyskryminacyjną oraz rzuty obiektów na prostą wyznaczoną przez wektor \(w\).

Rysunek 1: Obiekty zrzutowane na prostą wyznaczoną poprzez wektor \(w\) [opr. własne].

Problem wielu klas¶

Metodę Fishera dla dwu klas można uogólnić na przypadek większej liczby klas. Jako pierwsi uogólnienie to podali C. R. Rao w 1948 [Rao1948] oraz J. G. Bryan w 1951 [Bryan1951]. Zauważmy, że

gdzie \(\eta\) jest wektorem średnim dla wszystkich obserwacji. Macierz

możemy uznać za miarę zmienności międzygrupowej. Mówimy wówczas o macierzy kowariancji międzygrupowej. Powyższą macierz oznaczamy symbolem \(S_B\), tzn.

Ponadto, niech \(S_W\) oznacza macierz postaci

gdzie \(p_i\) jest prawdopodobieństwem a priori \(i\)-tej klasy, natomiast \(S_i\) oznaczają próbkową macierz kowariancji w klasie \(i\). Stąd na podstawie (6) i (7) kryterium Fishera (5) możemy zapisać w następującej, równoważnej, postaci

Uogólnienie algorytmu FLD dla większej liczby klas sprowadza się więc do uogólnienia wyrażeń (6) i (7). Wówczas wyrażenie (6) dla liczby klas \(L>2\) jest postaci

natomiast wyrażenie (7) przyjmuje postać

gdzie \(S_i\) jest macierzą rozproszenia wewnątrzklasowego dla \(i\)-tej klasy. Otrzymujemy w ten sposób uogólnioną liniową dyskryminację Fishera dla liczby klas \(L>2\).

Metodami opartymi na kryterium Fishera zajmował się między innymi W. Malina [Malina1981], [Malina1987], [Malina2001], [Kolakowska2005], a także Okada i Tomita [Okada1984].

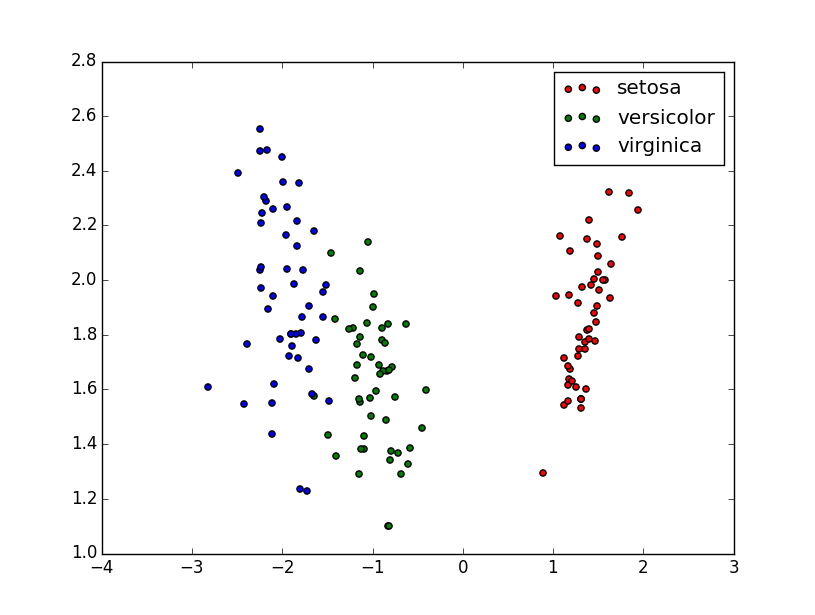
Przykład 9

Rozważmy zbiór danych Iris. W zbiorze znajduje się 150 obiektów z trzech różnych gatunków irysów, a każdy z nich jest charakteryzowany przez cztery cechy: długość (w \(cm\).) listka kielicha kwiatowego, szerokość (w \(cm\)) listka kielicha kwiatowego, długość (w \(cm\)) płatka kwiatu, szerokość (w \(cm\)) płatka kwiatu. Wykorzystamy teraz algorytm FLD do redukcji wymiaru przestrzeni cech do dwóch. Wizualizacja wyników działania algorytmu FLD na zbiorze Iris została przedstawiona na rysunku 2. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę.

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.lda import LDA

#importujemy zbiór danych
iris = datasets.load_iris()

X = iris.data       #macierz obiektór
y = iris.target     #wektor ich poprawnej klasyfikacji
target_names = iris.target_names    #nazwa klasy obiektu

#Uruchamiamy algorytm FLD dla 2 komponentów
lda = LDA(n_components=2, solver="eigen")
X_r2 = lda.fit(X, y).transform(X)

#Tworzymy wykres
plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], target_names):
    plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], c=c,
                label=target_name)
plt.legend()
plt.show()

Rysunek 2: Wizualizacja wyników działania algorytmu FLD na zbiorze Iris [opr. własne].

Metoda składowych głównych (PCA)¶

Jednym z najbardziej znanych algorytmów ekstrakcji cech jest analiza komponentów głównych (ang. Principal Copmonent Analysis (PCA)) (por. Jolliffe [Jolliffe2002], Koronacki [Koronacki2005], Cooley [Cooley1971]). Algorytm ten umożliwia transformację danych z wejściowej przestrzeni cech \(\mathbb{R}^p\) do danych z przestrzeni \(\mathbb{R}^d\) przy czym \(d<p\) tak, by zmienność rzutowanych danych mierzona sumą wariancji była największa. Otrzymane w wyniku działania tej metody nowe cechy są kombinacjami liniowymi oryginalnych cech zbioru uczącego. W metodzie tej zakładamy, że dysponujemy pewnym zbiorem uczącym \(X\), jednak nie musimy posiadać informacji o przynależności klasowej próbek z tego zbioru. Ideą algorytmu PCA jest optymalizacja następującej funkcji celu

przy warunkach

Do optymalizacji powyższej funkcji celu wykorzystujemy następujące twierdzenie

Dowód powyższego twierdzenia można znaleźć w [Koronacki2005].

Na podstawie tego twierdzenia zadanie wyznaczenia komponentów głównych sprowadza się do wyznaczenia wektorów własnych macierzy kowariancji \(\Sigma\). Metodę PCA przedstawiamy na poniższym schemacie (algorytm 6).

Wektor własny odpowiadający \(k\) -tej największej wartości własnej nazywamy \(k\) -tym komponentem głównym. Udowodniono, że kolejne komponenty główne wyznaczają kolejne kierunki największej w sensie wariancji zmienności wektora cech (por. Koronacki [Koronacki2005]). Ponadto, suma wszystkich wartości własnych macierzy kowariancji \(\Sigma\) jest równa sumie wariancji współrzędnych. Aby stwierdzić możliwość redukcji wymiaru przestrzeni cech oraz jej wielkość należy zastosować pewne kryterium. Kryterium to oparte jest na własnościach macierzy symetrycznej. Ponieważ ślad macierzy jest równy sumie wszystkich wartości własnych, zatem suma wszystkich wartości własnych macierzy kowariancji \(\Sigma\) jest równa sumie wariacji poszczególnych współrzędnych. Stąd procent zmienności mierzony wariancją zmierzony przez \(k\) pierwszych komponentów głównych wyraża się wzorem

Ponadto, uzyskana w wyniku zastosowania metody PCA przestrzeń ma następującą cechę. Zastosowana transformacja elementów zbioru uczącego minimalizuje odległości pomiędzy wektorami obserwacji a rzutami, tj.

gdzie \(d(x_i, x_j)\) jest metryką Euklidesa pomiędzy wektorami \(x_i, x_j\), wektory \(x_i^{\star}, x_j^{\star}\) są obrazami wektorów zbioru uczącego \(x_i, x_j\). Ponieważ przy rzutowaniu danych na przestrzeń o niższym wymiarze odległości nie mogą wzrosnąć, w powyższym wzorze można nie uwzględniać modułu różnic odległości.

W praktycznych zastosowaniach jedną z metod ustalania ilości komponentów polega na wybraniu takiej ich liczby aby łącznie wyjaśniały minimum 80% zmienności wariancji.

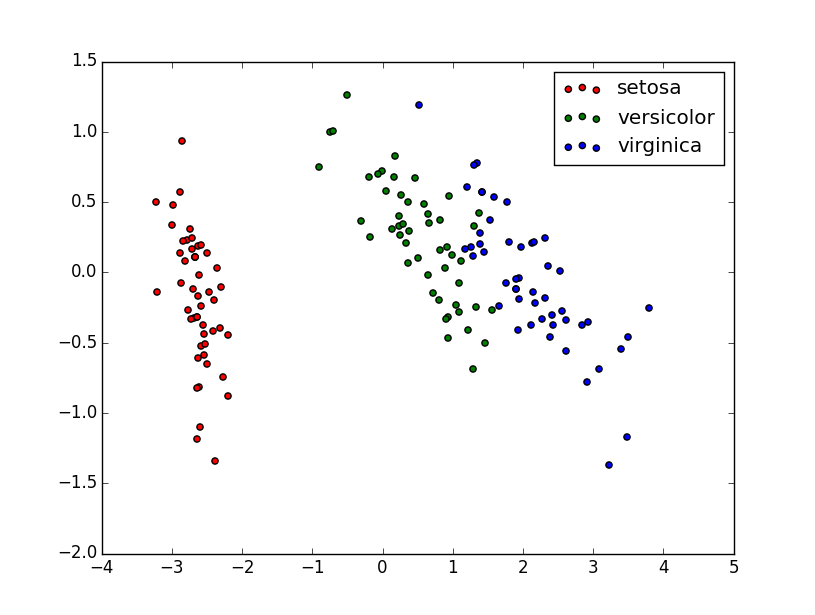
Przykład 9

Rozważmy zbiór danych Iris. W zbiorze znajduje się 150 obiektów z trzech różnych gatunków irysów, a każdy z nich jest charakteryzowany przez cztery cechy: długość (w \(cm\).) listka kielicha kwiatowego, szerokość (w \(cm\)) listka kielicha kwiatowego, długość (w \(cm\)) płatka kwiatu, szerokość (w \(cm\)) płatka kwiatu. Wykorzystamy teraz algorytm PCA do redukcji wymiaru przestrzeni cech do dwóch. Pierwszy z komponentów wyjaśnia 92,46% zmienności wariancji, natomiast drugi z nich wyjaśnia 5.3%. Łącznie oba komponenty wyjaśniają 97,76% zmienności wariancji. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę.

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.lda import LDA

#importujemy zbiór danych
iris = datasets.load_iris()

X = iris.data       #macierz obiektór
y = iris.target     #wektor ich poprawnej klasyfikacji
target_names = iris.target_names    #nazwa klasy obiektu

#Uruchamiamy algorytm PCA dla 2 komponentów
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)

#Procent wariancji wyjaśnianej przez metodę dla każdego komponentu
print('Współczynnik wyjaśnianej wariancji dla 2 komponentów: %s'
      % str(pca.explained_variance_ratio_))

#Tworzymy wykres
plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], target_names):
    plt.scatter(X_r[y == i, 0], X_r[y == i, 1], c=c,
                label=target_name)
plt.legend()
plt.show()

Rysunek 3: Wizualizacja wyników działania algorytmu PCA na zbiorze Iris [opr. własne].

Dekompozycja na wartości osobliwe (SVD)¶

Inną szeroko stosowaną metodą redukcji wymiaru przestrzeni cech jest dekompozycja na wartości osobliwe (ang. Singular Value decomposition (SVD)) (por. [Gentle1998], [Sarwar2000]).

Dowód znajduje się w [Kincaid2006].

Metoda SVD charakteryzuje się następującymi własnościami. Macierz \(U\) jest macierzą ortogonalną, której kolumny są wektorami własnymi macierzy \(XX^T\). Podobnie macierz \(W\) jest macierzą ortogonalną, której kolumny są wektorami własnymi macierzy \(X^TX\). Jeżeli macierz \(X\) jest macierzą nieosobliwą, to można tak dobrać macierze \(U\) oraz \(W\), żeby jej wszystkie wartości szczególne (osobliwe) były dodatnie. Jeżeli którakolwiek wartość szczególna macierzy \(X\) jest równa \(0\), to macierz ta jest macierzą osobliwą. Wartość bezwzględna wyznacznika kwadratowej macierzy \(X\) jest iloczynem jej wszystkich wartości szczególnych tzn

Metoda Cząstkowych Najmniejszych Kwadratów¶

Metoda Cząstkowych Najmniejszych Kwadratów (ang. Partial Least Squares (PLS)) znajduję liniową zależność pomiędzy dwoma macierzami, zwanymi również blokami, w celu znalezienia tzw. komponentów (zmiennych) ukrytych. Model ten ma postać

gdzie \(T\) jest macierzą komponentów, natomiast \(E\) jest macierzą resztkową. Poniżej przedstawimy ogólne założenia metody PLS. Załóżmy, że mamy macierze \(X\) oraz \(Y\) postaci:

Metoda PLS dokonuje ekstrakcji komponentów ukrytych \(T=[t_1,...,t_k]\). W metodzie tej bierzemy pod uwagę zarówno macierz danych wejściowych \(X\) jak i macierz odpowiedzi \(Y\). Ekstrakcji komponentów dokonujemy w taki sposób, aby kowariancja pomiędzy liniową kombinacją wektorów macierzy \(X\) a macierzą odpowiedzi była jak największa. W metodzie cząstkowych najmniejszych kwadratów maksymalizujemy zatem następującą funkcję celu

przy warunkach

Wektory \(t_k=X_{k-1}w_k\) oraz \(u_k=Y_{k-1}q_k\) nazywamy odpowiednio komponentami macierzy \(X\) oraz \(Y\), natomiast wektory \(w_k\) oraz \(q_k\) nazywamy wektorami wag odpowiednio dla macierzy \(X\) oraz \(Y\). Rysunek 4 przedstawia macierze i wektory występujące w metodzie PLS.

Rysunek 4: Reprezentacja macierzy występujących w metodzie PLS [opr. własne].

Metoda PLS znajduje zastosowanie w przypadku, kiedy mamy do czynienia z danymi wysoko skorelowanymi, a także z tzw. fat data czyli danymi, gdzie ilość zmiennych znacznie przewyższa ilość próbek. W szczególności metoda ta sprawdza się w zagadnieniach chemometrii, eksperymentach mikromacierzowych, eksperymentach EEG (elektroencyfalogram), ale także w ekonomii oraz badaniach marketingowych. Metoda cząstkowych najmniejszych kwadratów była przedmiotem badań wielu naukowców na przestrzeni ostatnich 40 lat. Poniżej przytaczamy kilka ważnych dat:

• Wold H. (1966, 1975) - Nonlinear Iterative Partial Least Squares (NIPALS) patrz [Wold1966], [Wold1975],
• Wold S. (1983) - PLS1 patrz [Wold1982],
• Höskuldsson (1988) - właściwości PLS [Hoskuldsson1988],
• Helland (1988),
• Rosipal, Trejo (2001) - kernel PLS [Rosipal2001],
• Bastien (2005) - uogólniona liniowa regresja PLS [Bastien2005].

Należy w tym miejscu nadmienić, że metoda PLS jest krytykowana za trudny do interpretacji model. Zrodziło się nawet pytanie czy jest to model statystyczny czy tylko prosty algorytm. Na powyższy model (8) należy raczej patrzeć jako na rodzaj dekompozycji macierzy niż na konkretny model matematyczny. Ponadto krytykę budzi również fakt, że trudno jest zinterpretować deflację macierzy, a także zależności pomiędzy predyktorami obliczone na jej podstawie oraz macierzą odpowiedzi. Próby zbadania aspektów statystycznych metody PLS w jej zastosowaniu do analizy regresji podjęte zostały w pracach Helland [Helland1990], [Helland2001], [Helland2004].

Regresja PLS - przypadek jednowymiarowy¶

Załóżmy, że macierz odpowiedzi math:Y jest wymiaru math:ntimes 1, tzn.

\[\begin{split}Y=\left[\begin{array}{c} y_{1}\\ y_{2}\\ \vdots\\ y_{n}\\ \end{array}\right]\!.\end{split}\]

Metody PLS są z powodzeniem stosowane jako metody klasyfikacji, regresji bądź też jako algorytmy zmniejszające wymiar przestrzeni cech. Metody te stosujemy kiedy dane, z którymi mamy do czynienia są wysoko współliniowe oraz kiedy liczba cech przekracza liczbę próbek. W pracach Geladi, Kowalski [Geladi1986], Tenenhaus [Tenenhaus1998], Wold [Wold2001] można znaleźć ogólne informacje o metodzie PLS. Statystyczne aspekty tej metody opisywane są w pracach Hellanda [Helland1988], [Helland1990], [Helland2001], Garthwaite’a [Garthwaite1994] oraz H”oskuldssona [Hoskuldsson1988], [Hoskuldsson2001]. Metoda PLS często znajduje zastosowanie w takich dziedzinach nauki jak chemometria (dziedzina chemii zajmująca się analizą danych chemicznych, fizycznych, medycznych w celu wyboru optymalnych procedur eksperymentalnych oraz do pozyskania wiedzy o układach chemicznych). Na temat zastosowań PLS w chemometrii istnieje duża liczba publikacji. Wystarczy wspomnieć monografię [Martens1989] czy prace [Wold1982], [Wold2001], [Briandet1996], [Frank1993]. Innym polem zastosowań metody PLS są problemy diagnostyki medycznej takie jak tzw. eksperymenty NIR (ang. Near Infra-Red), czyli eksperymenty oparte na analizie sygnału promieniowania w bliskiej podczerwieni odbitego od powierzchni mózgu, eksperymenty mikromacierzowe zajmujące się analizą genów czy badania EEG (elektroencyfalogram). Również tutaj opublikowano wiele prac, w tym artykuły autorstwa Nguyen, Rocke [Nguyen2002], [Nguyen2002] oraz [Fort2004]. Metody oparte na algorytmie PLS znajdują również zastosowanie w edukacji. Warto tutaj wymienić prace Sellin, Versand [Sellin1995] oraz Noonan [Noonan1979], [Noonan1983]. Ponadto, metody te stosuje się szeroko w ekonomii i badaniach rynku [Fornell1984], [Fornell1994], [Hulland1999]. We wszystkich tych przypadkach cechą wspólną jest duża, a czasami wręcz ogromna, liczba cech w stosunku do małej liczby próbek.

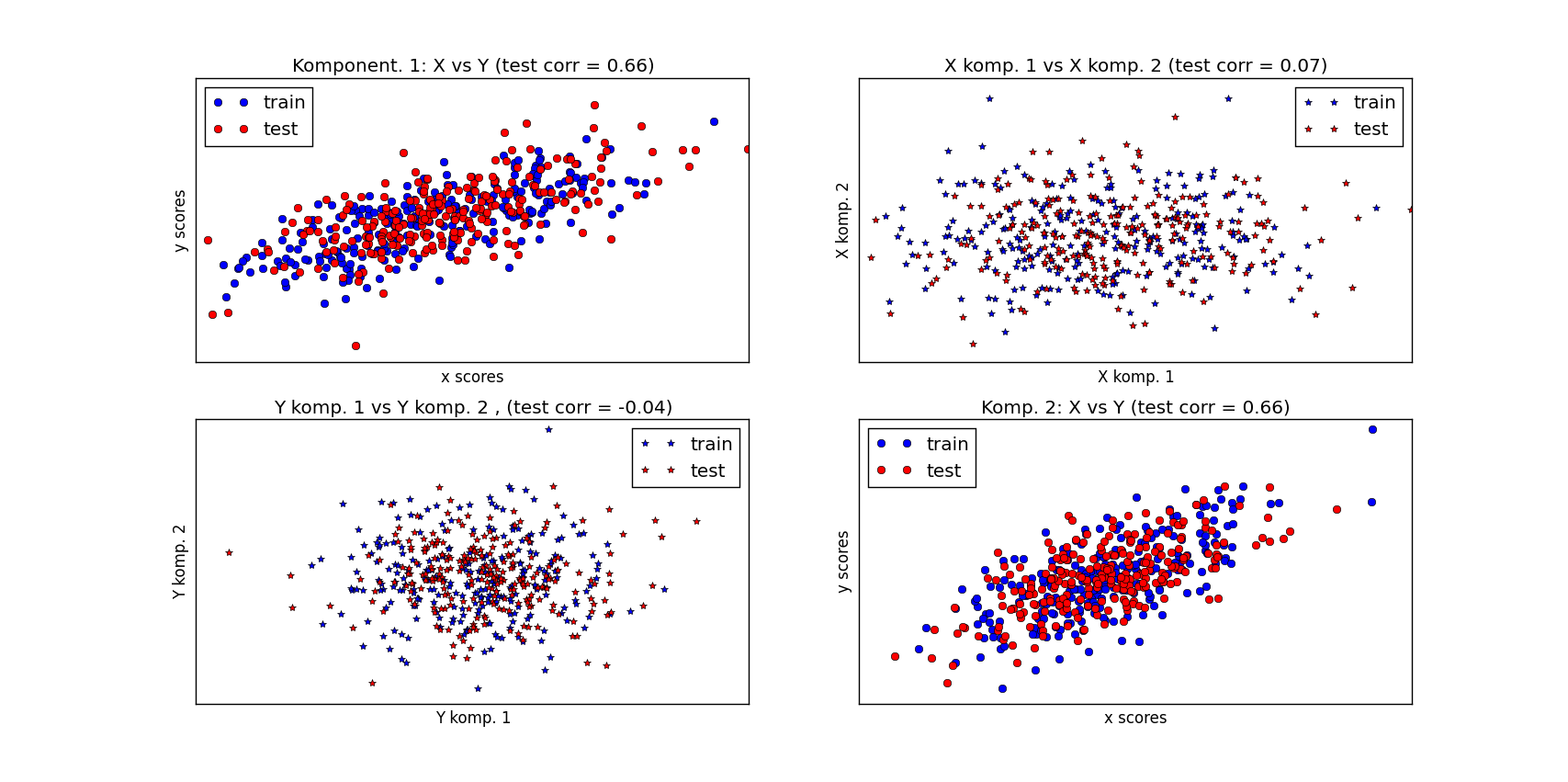
Przykład 11

Działanie algorytmu PLS pokażemy na następującym przykładzie. Zbiór danych zawiera \(500\) obiektów charakteryzowanych przez \(4\) cechy i został losowo wygenerowany z rozkładu normalnego. Zbiór ten dzielimy w połowie na część uczącą i testową. Wyznaczamy wektor wag na zbiorze uczącym a następnie dokonujemy redukcji wymiaru przestrzeni cech na zbiorze testowym. Wyniki umieszczamy na wykresie Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę.

import numpy as np
import pylab as pl
from sklearn.cross_decomposition import PLSCanonical
##########################################################
#Tworzymy zbiór danych

n = 500
#Tworzymy 2 zmienne:
l1 = np.random.normal(size=n)
l2 = np.random.normal(size=n)

latents = np.array([l1, l1, l2, l2]).T
X = latents + np.random.normal(size=4 * n).reshape((n, 4))
Y = latents + np.random.normal(size=4 * n).reshape((n, 4))

#Tworzymy zbiór uczący i testowy
X_train = X[:n / 2]
Y_train = Y[:n / 2]
X_test = X[n / 2:]
Y_test = Y[n / 2:]

print np.shape(Y_train)
print np.shape(X)

print("Corr(X)")
print(np.round(np.corrcoef(X.T), 2))
print("Corr(Y)")
print(np.round(np.corrcoef(Y.T), 2))

#############################################################
# Algorytm PLS

#Wyznaczamy wektor wag
plsca = PLSCanonical(n_components=2)
plsca.fit(X_train, Y_train)

#Redukujemy wymiar przestrzeni cech
X_train_r, Y_train_r = plsca.transform(X_train, Y_train)
X_test_r, Y_test_r = plsca.transform(X_test, Y_test)

#Wyniki umieszczamy na wykresie.
# 1) On diagonal plot X vs Y scores on each components
pl.figure(figsize=(12, 8))
pl.subplot(221)
pl.plot(X_train_r[:, 0], Y_train_r[:, 0], "ob", label="train")
pl.plot(X_test_r[:, 0], Y_test_r[:, 0], "or", label="test")
pl.xlabel("x scores")
pl.ylabel("y scores")
pl.title('Komponent. 1: X vs Y (test corr = %.2f)' %
         np.corrcoef(X_test_r[:, 0], Y_test_r[:, 0])[0, 1])
pl.xticks(())
pl.yticks(())
pl.legend(loc="best")

pl.subplot(224)
pl.plot(X_train_r[:, 1], Y_train_r[:, 1], "ob", label="train")
pl.plot(X_test_r[:, 1], Y_test_r[:, 1], "or", label="test")
pl.xlabel("x scores")
pl.ylabel("y scores")
pl.title('Komp. 2: X vs Y (test corr = %.2f)' %
         np.corrcoef(X_test_r[:, 1], Y_test_r[:, 1])[0, 1])
pl.xticks(())
pl.yticks(())
pl.legend(loc="best")

# 2) Komponent 1 vs Komponent 2 zbiorów X i Y
pl.subplot(222)
pl.plot(X_train_r[:, 0], X_train_r[:, 1], "*b", label="train")
pl.plot(X_test_r[:, 0], X_test_r[:, 1], "*r", label="test")
pl.xlabel("X komp. 1")
pl.ylabel("X komp. 2")
pl.title('X komp. 1 vs X komp. 2 (test corr = %.2f)'
         % np.corrcoef(X_test_r[:, 0], X_test_r[:, 1])[0, 1])
pl.legend(loc="best")
pl.xticks(())
pl.yticks(())

pl.subplot(223)
pl.plot(Y_train_r[:, 0], Y_train_r[:, 1], "*b", label="train")
pl.plot(Y_test_r[:, 0], Y_test_r[:, 1], "*r", label="test")
pl.xlabel("Y komp. 1")
pl.ylabel("Y komp. 2")
pl.title('Y komp. 1 vs Y komp. 2 , (test corr = %.2f)'
         % np.corrcoef(Y_test_r[:, 0], Y_test_r[:, 1])[0, 1])
pl.legend(loc="best")
pl.xticks(())
pl.yticks(())
pl.show()

Rysunek 5: Wizualizacja wyników działania algorytmu PLS [opr. własne].

Algorytm PLS1¶

Algorytm PLS1 zaproponowany został przez S. Wolda, syna H. Wolda, w 1983 (por. [Wold1982]). Dokonuje on ekstrakcji wektora wag \(w_k\) oraz komponentów \(t_k\), a następnie oblicza wektory \(p_k=X_{k-1}^Tt_k\) oraz \(q_k=Y^Tt_k\). Takie podejście pozwala na wykonanie biliniowej dekompozycji danej wzorami (9) oraz (10). Algorytm PLS1 przedstawiamy na schemacie 8.

Zauważmy, że wartości \(q_n\) wymiaru \(n\times 1\) są współczynnikami regresji \(t_k\) na \(Y\). Macierz wszystkich współczynników regresji uzyskanych w \(k\) iteracjach oznaczamy symbolem \(\hat{q}_k=(q_1,...,q_k)\). Współczynniki te uzyskujemy metodą najmniejszych kwadratów. Następnie wektor \(\hat{q}_k\) transformujemy z powrotem do oryginalnych zmiennych, dzięki czemu otrzymujemy wektor współczynników regresji wymiaru \(p\times 1\). Wektor ten oznaczamy poprzez \(B_k^{PLS}\). Współczynniki te są dane wzorem

gdzie \(W=(w_1,\cdots,w_k)\), \(P=(p_1,\cdots,p_k)\), oraz \(\hat{q}\) silnie zależą od macierzy odpowiedzi \(Y\). Stopień złożoności metody PLS jest kontrolowany poprzez liczbę komponentów \(t_k\) w modelu regresji. Wybór wartości \(k\) ma wpływ nie tylko na złożoność modelu lecz również na jego sprawność.

Dowód znajduje się w pracy Höskuldsson [Hoskuldsson1988].

Algorytm ten możemy również zapisać za pomocą narzędzi statystycznych w sposób, który przedstawiany na schemacie (algorytm 9).