Układy funkcyjne i sekwencyjne¶
Cel ćwiczenia¶
Celem ćwiczenia jest poznanie realizacji funkcji logicznych przy pomocy dekoderów, multiplekserów oraz sumatorów scalonych TTL i CMOS oraz projektowanie i budowa układów logicznych powszechnie stosowanych w automatyce i technice cyfrowej.
Wymagane wiadomości¶
Znajomość budowy funkcji logicznych przy pomocy układów funkcyjnych i sekwencyjnych, umiejętność stosowania kodów cyfrowych i praw techniki cyfrowej.
Układy cyfrowe mogą przetwarzać informację tylko w postaci binarnej, zatem do realizacji operacji matematycznych można wykorzystać tylko liczby przedstawione w postaci binarnej. Sposoby przedstawiania liczb zakłada konieczność przejścia z systemu dziesiętnego na binarny tabela poniżej. Naturalny kod dwójkowy (NKB) – system pozycyjny \(p=2\) (podstawa systemu), zbiór znaków: \(a\in\{0, 1\}\).
liczby dodatnie – postać taka sama niezależnie od zapisu liczby ujemne – przy stałej długości słowa mogą mieć różną postać
- zapis „znak – moduł” – najstarszy bit ma wartość 1,
- uzupełnienie do jedności – negacja,
- uzupełnienie do dwóch – najstarszy bit ma wagę ujemną, pozostała część liczby zapisana jest w normalnym kodzie dwójkowym.
Korzystając z zapisu w dowolnym kodzie należy zwrócić uwagę na działania funkcji logicznych w tych kodach. Dlatego realizacja dowolnej funkcji może mieć wiele rozwiązań stanów.
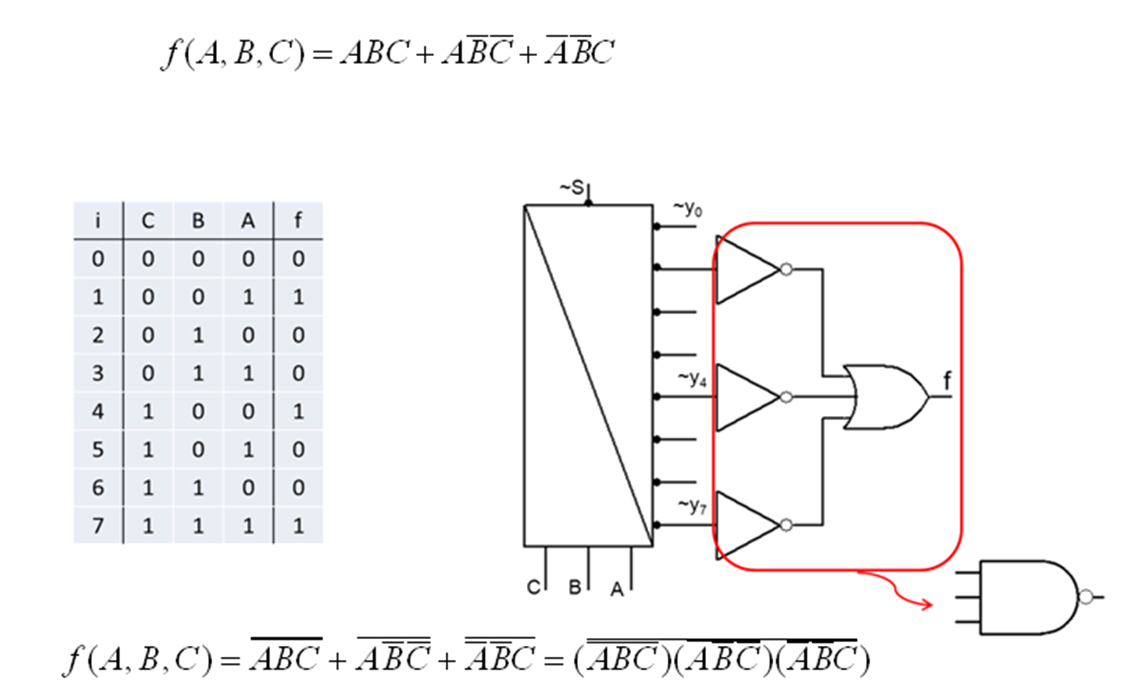
Przykład realizacji funkcji przy użyciu dekodera
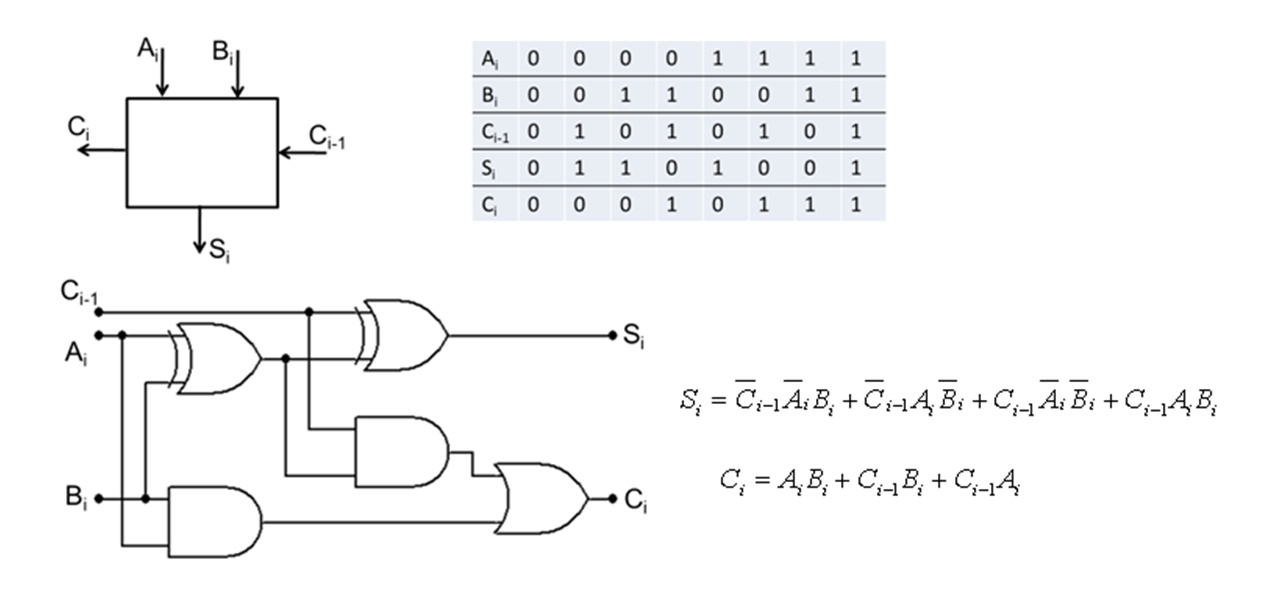
Sumator jednobitowy
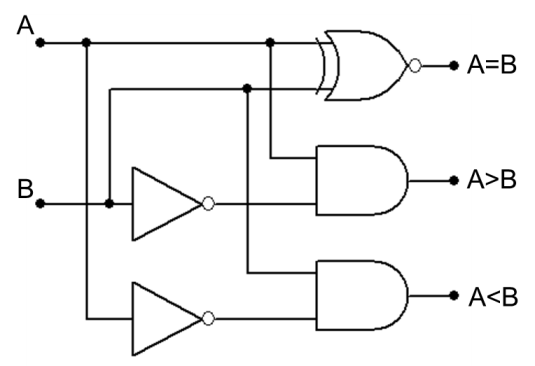
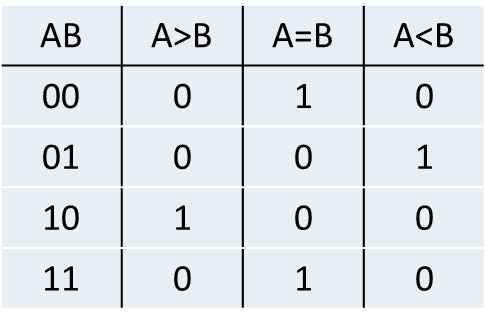
Zwykły sumator służy jedynie do dodawania modułów liczb, jednakże przy dodawaniu algebraicznym trzeba brać pod uwagę znaki liczb. Konieczne jest zastosowanie komparatora znaków.
 |
 |
Korzystając z opisów i przykładów powyżej należy wykonać operacje na bitach dla poszczególnych funkcji logicznych i liczb w odpowiednich kodach na układach funkcyjnych.
Przebieg ćwiczenia¶
Badanie podstawowych funkcji przy użyciu dekodera (o wyborze funkcji decyduje prowadzący):
\(y(X_1X_2X_3)=X_1X_2X_3+X_1\overline{X_2}X_3+\overline{X_1} \overline{X_2}X_3\)
\(y(X_1X_2X_3)=(X_1+X_2)(\overline{X_2}+X_3)(X_2+X_3)\)
\(y(X_1X_2X_3)-(\overline{X_1+X_2})X_2\overline{X_3}+\overline{X_1} \overline{X_2} \overline{X_3}+(\overline{X_2} \overline{X_3}+X_2X_3)X_1\)
n \(X_1\) \(X_2\) \(X_3\) \(X_4\) \(y_{teor.}\) \(y_{zm.}\) 0 \(0\) \(0\) \(0\) \(0\) 1 … (środowisko LabVIEW lub CEDAR Logic).
Sumator jednobitowy jako element realizujący określone funkcje logiczne
Przebadać jeden sumator jednobitowy, wypełniając poniższe tabele. Pierwsza z nich dotyczy funkcji jednoargumentowych:
\(S=f(A)\) lub \(S=f(B)\)
Warunek funkcja Nazwa f. Boolowskiej \(C_0=0,B=1\) \(A\) \(S=f(A)\) \(0\) \(1\) \(C_0=0,A=1\) \(B\) \(S=f(B)\) \(0\) \(1\) \(C_0=1,B=0\) \(A\) \(S=f(A)\) \(0\) \(1\) \(C_0=1,A=0\) \(B\) \(S=f(B)\) \(0\) \(1\) Natomiast druga dotyczy funkcji dwuargumentowych: \(C_i=f(A,B)\) i \(S=f(A,B)\)
Warunek funkcja Nazwa f. Boolowskiej \(C_0=1\) \(A\) \(B\) \(C_i=f(A,B)\) \(0\) \(0\) \(0\) \(1\) \(1\) \(0\) \(1\) \(1\) \(C_0=0\) \(A\) \(B\) \(C_i=f(A,B)\) \(0\) \(0\) \(0\) \(1\) \(1\) \(0\) \(1\) \(1\) \(C_0=1\) \(A\) \(B\) \(S=f(A,B)\) \(0\) \(0\) \(0\) \(1\) \(1\) \(0\) \(1\) \(1\) \(C_0=0\) \(A\) \(B\) \(S=f(A,B)\) \(0\) \(0\) \(0\) \(1\) \(1\) \(0\) \(1\) \(1\) Realizacja układu kombinacyjnego przy użyciu sumatorów jednobitowych.
Używając tylko sumatorów jednobitowych można budować takie układy kombinacyjne, które realizują funkcje boolowskie zawierające działania typowe dla sumatorów, to znaczy różnicę symetryczną, sumę i iloczyn logiczny a jednocześnie nie wymagają użycia dużej liczby negacji. Zamodelować niżej podaną funkcję \(Y(X_1X_2X_3X_4)\) używając jedynie sumatorów jednobitowych. Sporządzić schemat generatora zadanej funkcji oraz wypełnić tabelę zależności. Ostatnią kolumnę wypełnić na podstawie pomiarów.
\[\begin{split}Y(X_1X_2X_3X_4) &= \overline{X_1}\overline{X_2}X_3X_4+\overline{X_1} X_2\overline{X_3}X_4+\overline{X_1}X_2X_3X_4\\ &+X_1\overline{X_2} \overline{X_3}X_4+X_1\overline{X_2}X_3X_4 + X_1X_2X_3X_4\\ &=X_4(X_3+X_1\oplus X_2)\end{split}\]Badanie sumatora ośmiobitowego.
Wykonać sumator ośmiobitowy z sumatorów czterobitowych. Wprowadzić dwie liczby w postaci binarnej nie większe niż 255 jako dodajnik i dodajna używają przełączników \(X_0-X_7\) i \(Y_0-Y_7\). Wynik należy obserwować na ośmiu diodach dołączonych do sumatora oraz na wyjściu \(C_i\). Na wybranych liczbach dokonać wszystkich możliwych operacji dodawania i odejmowania. Operacje wykonać na liczbach przedstawionych w postaci:
- znak moduł,
- uzupełnienie do 1,
- uzupełnienie do 2
Opracowanie wyników¶
W sprawozdaniu:
- Sporządzić schematy badanych funkcji przy pomocy dekodera wraz z tabelą działania.
- Sporządzić schematy badanych układów z użyciem sumatorów jednobitowych wraz z tabelą działania. Rozpisać procedurę upraszczania funkcji realizowanej w punkcie 2. Narysować schemat analogu funkcji realizowanej przez sumator z symbolem funkcji i tabelą działania modelującego tę funkcję przy użyciu sumatorów.
- Sporządzić schemat logiczny dla zbadanej funkcji przy użyciu sumatorów jednobitowych wraz z tabelą działania.
- Narysować schemat sumatora ośmiobitowego złożonego z jednostek jednobitowych i opisać sygnały 0-1 na poszczególnych zaciskach dla dowolnego przykładu dodawania dwóch liczb.
Literatura¶
| [Filpkowski2005-4] | A. Filpkowski, „Ukady elektroniczne analogowe i cyfrowe” EIT 2005r. |
| [Kalisz2002-4] | J. Kalisz, „Podstawy elektroniki cyfrowej” WKŁ 2002r |
| [Horowitz2002-4] | P. Horowitz, W Hill, „Sztuka elektroniki” WKŁ 2002r. |
| [Pioro2005-4] | M. Pióro, „Podstawy elektroniki” WSiP 2005r. |
| [Chwaleba2002-4] | A. Chwaleba, „Pracownia elektroniczna” WSiP 2002r. |
| [Pioro1996-4] | M. Pióro „Podstawy elektroniki, część I i część II”, Warszawa 1996, |
| [Piecha1985-4] | J. Piecha, „Elementy cyfrowe TTL” Skrypt Uniwersytetu Śląskiego 1985 |
Testy do rozdziału¶
Test 1¶
Test 2¶
Test 3¶
Test 4¶
Test 5¶
Test 6¶
Test 7¶
Test 8¶
Test 9¶
Test 10¶
Pytania kontrolne¶
- Jaki zapis liczby binarnej nie zmienia jej postaci w kodzie dziesiętnym
- Ilu bitów jest potrzebnych aby zapisać liczbę \(16\) w NKB
- Czy cyfra \(0\) w każdej reprezentacji binarnej ma taki sam zapis
- Czy jednostka ALU może składać się z sumatorów jednobitowych
- Czy dekoder pozwala realizować wszystkie funkcje logiczne
- Czy sumator jednobitowy wystarczy do realizacji każdego funktora
- Czy półsumator jednobitowy wystarczy do realizacji każdego funktora
- Jak zrealizować negację bitu przy użyciu sumatora jednobitowego
- Jaka jest różnica między sumą logiczną a arytmetyczną
- Jakie działanie realizuje sumą arytmetyczną