Definicje¶
Drzewem w informatyce nazywamy skierowany, acykliczny graf spójny. Jest to zatem struktura składająca się ze zbioru wierzchołków oraz krawędzi łączących wierzchołki ze sobą. Krawędzie drzewa nazywa się gałęziami. W grafie skierowanym istotny jest kierunek połączenia, to znaczy rozróżniamy wierzchołek z którego krawędź wychodzi i do którego jest skierowana. Przyjmujemy, że każdy poza jednym wierzchołek ma dokładnie jedną krawędź wchodzącą, natomiast liczba krawędzi wychodzących przekracza jedną, bądź nie ma ich wcale. Jedyny wierzchołek drzewa do którego nie wchodzi żadna krawędź nazywamy korzeniem drzewa, natomiast każdy wierzchołek z którego żadna krawędź nie wychodzi nazywamy liściem.
W rozpatrywanym tutaj aspekcie struktura drzewa klasyfikacyjnego (decyzyjnego, decyzyjne) w sposób graficzny reprezentuje klasyfikator, a więc funkcję która wektorowi cech obiektu przypisuje etykietę klasy. Realizowane jest to przez nadanie specjalnego znaczenia elementom drzewa i tak węzły reprezentują testy przeprowadzane na wartościach atrybutów próbek zbioru uczącego, krawędzie reprezentują możliwe wyniki tych testów a liście utożsamiane są z etykietami klasowymi. Dokonanie klasyfikacji konkretnej próbki odbywa się poprzez przejście ścieżki od korzenia do któregoś z liści drzewa poprzez przeprowadzenie testów w kolejnych węzłach i poruszanie się krawędziami zgodnymi z wynikami tych testów.
Przykład tego podejścia ilustruje rysunek 1. Po lewej stronie zaznaczono obiekty zbioru uczącego w dwuwymiarowej przestrzeni cech złożonej z atrybutów \(x_1\), \(x_2\). Elementy klasy 1 zaznaczono kwadratem natomiast klasy 2 kółkiem. Po prawej stronie umieszczono proste drzewo decyzyjne realizujące rozważany problem klasyfikacyjny. Przydzielenie próbki do klasy odbywa się poprzez przejście drzewa od korzenia do liścia poprzez wykonanie na wartościach atrybutów testów widocznych w węzłach. Jeśli więc wartość atrybutu \(x_1>0.8\) to klasyfikowany element zostaje przydzielony do klasy 2, w przeciwnym wypadku należy przetestować wartość atrybutu \(x_2\) i w zależności od niej zaklasyfikować element do jednej z klas.
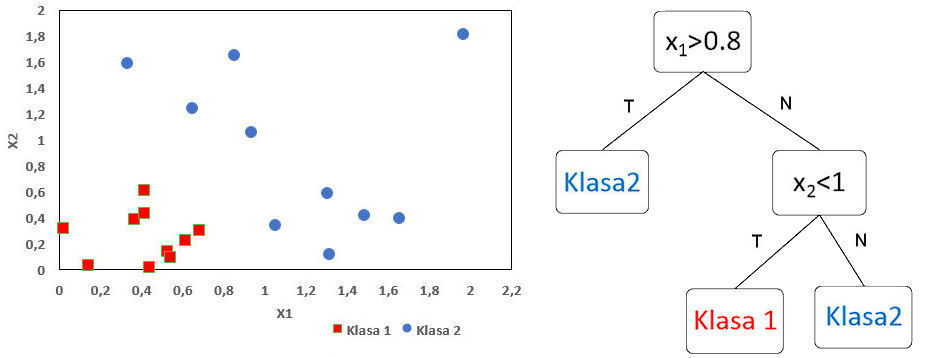
Rysunek 1: Drzewo klasyfikacyjne dla przykładowego problemu klasyfikacyjnego. Źródło: opracowanie własne
Zauważmy, że wykonanie każdego z testów zbiór uczący dzieli podgrupy. Uczenie algorytmu drzewa klasyfikacyjnego polega na zbudowaniu drzewa a zatem na podaniu testów jakim należy poddać atrybuty wektora cech klasyfikowanego obiektu aby podjąć decyzję dotyczącą jego przynależności klasowej. W rozważanym przykładzie uzyskane drzewo jest drzewem binarnym, w ogólnym przypadku tak być nie musi. W szczególności w przypadku rozważania atrybutów jakościowych liczba wyników testu może być równa liczbie rozważanych kategorii. Przykładem może być atrybut wykształcenie, w przypadku którego każdej wartości (podstawowe, średnie, wyższe) może odpowiadać odpowiednia gałąź drzewa decyzyjnego.
Formalnie drzewo decyzyjne opisuje poniższa definicja rekurencyjna [Cichosz2007]:
Definicja 10
Niech dany będzie problem klasyfikacyjny o zbiorze klas \(C\) dla dziedziny \(X\) o atrybutach \(a_1,...,a_p\).
- Liść zawierający dowolną etykietę kategorii \(y\in C\) jest drzewem decyzyjnym.
- Jeżeli \(t:X\to {{R}_{t}}\) jest testem przeprowadzanyn na wartościach atrybutów przykładów o zbiorze możliwych wyników \(R_t=\{r_1,...,r_m\}\) oraz \(T_1,...,T_m\) są drzewami decyzyjnymi, to węzeł zawierający test \(t\), z którego wychodzi \(m\) gałęzi w ten sposób, że \(i\)-ta gałąź odpowiada wynikowi \(i\)-tego testu dla \(i=1,...,m\) i prowadzi do drzewa \(T_i\), jest drzewem decyzyjnym.
Dla dowolnego zbioru próbek uczących \(X_{train}\) każdemu węzłowi drzewa decyzyjnego można przypisać podzbiór składający się ze wszystkich elementów dla których dany węzeł zostanie osiągnięty w trakcie ich klasyfikacji. Takie elementy będziemy nazywać związanymi z odpowiednim węzłem bądź liściem. Pojęcie to w sposób formalny definiujemy poniżej.
Definicja 11
Niech dane będzie drzewo decyzyjne \(T\) ze zbiorem węzłów \(N_T\) oraz zbiorem liści \(L_T\). Mówimy, że obiekt \(x \in X\):
- jest związany z liściem (odpowiada liściowi) \(leaf \in Leaves_T\) drzewa decyzyjnego \(T\), jeśli w procesie klasyfikacji klasyfikacji elementu \(x\) za pomocą drzewa \(T\) osiągany jest ten liść.
- jest związany z węzłem (odpowiada węzłowi) \(node \in Nodes_T\) drzewa decyzyjnego \(T\), jeśli w procesie klasyfikacji elementu \(x\) za pomocą drzewa \(T\) węzeł \(node\) znajduje się na ścieżce łączącej korzeń drzewa \(T\) z liściem odpowiadającym elementowi \(x\).
Każdej klasyfikowanej próbce zbioru uczącego czy testowego odpowiada dokładnie jeden liść z nią związany, który oznaczmy \(leaf_{T,x}\) oraz zbiór związanych z nią węzłów \(Nodes_{T,x}\), przy czym na każdym poziomie drzewa taki węzeł jest tylko jeden.