Konstrukcja drzew klasyfikacyjnych¶

Kryterium stopu¶

Kryterium stopu sprawdzane jest przy każdym wywołaniu rekurencyjnej procedury budowy drzewa. Zauważmy, że przebiegając po drzewie wraz z odwiedzaniem jego kolejnych poziomów maleje liczba przypadków uczących związanych z analizowanym węzłem. Naturalnym kryterium stopu jest przynależność wszystkich próbek uczących związanych z węzłem do jednej klasy. W praktyce stosowanie takiego kryterium może prowadzić do generowania drzew o zbyt złożonej strukturze. Ponadto wraz z rozrastaniem się struktury drzewa maleje również liczebność zbioru możliwych testów do zastosowania na wartościach atrybutów zbioru uczącego, może się więc zdarzyć że na pewnym poziomie brak już możliwych testów do zastosowania. W takim przypadku w przypadku zaistnienia kryterium stopu etykietę związaną z liściem ustala się zgodnie z klasą najliczniej reprezentowaną wśród próbek uczących związanych z tym liściem. W rzeczywistości bardzo często kryterium stopu dobierane jest w ten sposób, że nie wymaga obecności tylko przykładów z jednej klasy dla utworzenia liścia, tylko powoduje jego utworzenie gdy jedna klas jest w znacznym stopniu dominująca. Zwróćmy uwagę, że kryterium stopu powinno być tak dobrane aby nie doszło do zjawiska przeuczenia i aby zdolności uogólniające budowanego klasyfikatora były jak największe.

Wybór testu¶

Operacja wyboru testu dla węzła drzewa klasyfikacyjnego jest kluczowym elementem każdego zstępującego algorytmu budowy drzewa o schemacie (Algorytm 3). To ona w największym stopniu decyduje w własnościach uzyskanego rozwiązania. Operacja ta polega na wybraniu testu najbardziej użytecznego dla analizowanego węzła, który będzie najbardziej użyteczny w rozpatrywanym zadaniu klasyfikacyjnym.

Zasadniczo możemy wyróżnić testy oparte o wiele bądź o pojedynczy atrybut. Ten drugi typ jest znacznie częściej stosowany. Rozpatrując możliwe wyniki testu najpopularniejszym rozwiązaniem jest stosowanie testów binarnych, to znaczy takich które mają tylko dwa możliwe wyniki. Stosowanie tego typu testów prowadzi do konstrukcji binarnego drzewa klasyfikacyjnego. Poniżej przedstawiamy najważniejsze testy dla wartości atrybutów.

1. Testy dla atrybutów nominalnych.

   W przypadku atrybutów nominalnych o niewielkiej liczbie możliwych wartości najprostszym rozwiązaniem jest test sprawdzający wartość atrybutu, a więc o wyniku będącym wartościom atrybutu. Taki test nazywa się tożsamościowym, bowiem faktycznie utożsamia test z wartością atrybutu, przykładowo dla atrybutu wykształcenie wynikiem testu może być podstawowe, średnie lub wyższe.

   Innym testem możliwym do zastosowania dla atrybutów nominalnych jest test tożsamościowy postaci:

   \[\begin{split}{{t}_{a}}\left( x \right)=\left\{ \begin{matrix} 1 & \text{gdy} & a\left( x \right)=v\\ 0 & \text{gdy} & a\left( x \right)\ne v\\ \end{matrix} \right.,\end{split}\]

   gdzie \(x\) jest wektorem uczącym poddawanym testowi oraz \(a\) testowanym atrybutem.

   Można rozpatrywać również testy przynależnościowe postaci:

   \[\begin{split}{{t}_{a}}\left( x \right)=\left\{ \begin{matrix} 1 & \text{gdy} & a\left( x \right)\in V\\ 0 & \text{gdy} & a\left( x \right)\notin V\\ \end{matrix} \right.,\end{split}\]

   gdzie \(V\) jest niepustym podzbiorem zbioru wartości atrybutu \(a\). W przypadku atrybutów nominalnych praktycznie wszystkie znane algorytmy uczenia drzew klasyfikacyjnych stosują jedynie testy tożsamościowe.

2. Testy dla atrybutów o charakterze ilościowym.

   W przypadku atrybutów dyskretnych o skończonej liczbie wartości można tutaj również stosować testy z poprzedniego punktu. W przypadku ciągłym można stosować testy przynależnościowe, gdzie zbiorem wartości jest przedział czy mnogościowa suma przedziałów. Najczęściej stosowanym testem w przypadku atrybutów ilościowych (jak również porządkowych) jest test nierównościowy postaci:

   \[\begin{split}{{t}_{a}}\left( x \right)=\left\{ \begin{matrix} 1 & \text{gdy} & a\left( x \right)\leq t\\ 0 & \text{gdy} & a\left( x \right)> t\\ \end{matrix} \right.,\end{split}\]

   gdzie \(t\) jest wartościową progową atrybutu.

Skupiamy się na testach opartych na wartościach pojedynczego atrybutu, w tym miejscu omówimy problem wyboru atrybutu na potrzeby testu. Najlepszym wyborem jest taki, który z jednej strony zapewnia maksymalną rozróżnialność elementów różnych klas w zbiorze uczącym a z drugiej jego użycie pozwala generować drzewo o prostej strukturze. Wybór atrybutu dokonywany jest za pomocą miar oceniających atrybuty, takich jak przyrost informacji. Jej wprowadzenie wymaga zdefiniowania pojęć entropii zbioru uczącego oraz jego entropii ze względu na test \(t\). Pojęcia te definiujemy poniżej.

Przy zastosowaniu miary przyrostu informacji dla wyboru testu wybieramy ze zbioru dostępnych testów ten, który maksymalizuje wspomnianą miarę. Zauważmy, że wartość entropii zbioru uczącego nie zależy od wyboru testu, zatem kryterium to jest równoważne minimalizacji entropii zbioru uczącego ze względu na test \(t\).

Inną bardzo popularną wyboru testu jest indeks Giniego ze względu na test \(t\), który wraz z miarą entropii wykorzystywany przez najbardziej popularny algorytm uczenia drzew klasyfikacyjnych a mianowicie algorytm CART (ang. Classification And Regression Tree). Wspomniany indeks definiujemy poniżej.

Przykład 7

W tym przykładzie prezentujemy sposób budowy drzewa klasyfikacyjnego dla zbioru danych iris. Drzewo zostanie zbudowane z użyciem parametrów domyślnych, w tym przypadku kryterium wyboru testu jest indeks Giniego. Skrypt języka Python realizujący to zadanie podajemy poniżej.

from sklearn.datasets import load_iris
from sklearn import tree

#wczytanie zbioru danych
iris = load_iris()

#drzewo klasyfikacyjne z domyślnymi wartościami parametrów
clf = tree.DecisionTreeClassifier()

#uczenie drzewa klasyfikacyjnego
clf = clf.fit(iris.data, iris.target)

#testowanie - klasyfikacja elementów zbioru uczącego
y=clf.predict(iris.data)
print 'Uzyskane w toku testowania etykiety:'
print y

#wygenerowanie pliku pdf repreentującego drzewo
#wymaga pakietu pydot oraz oprogramowania Graphviz
from sklearn.externals.six import StringIO
import pydot
dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf("drzewo_iris.pdf")

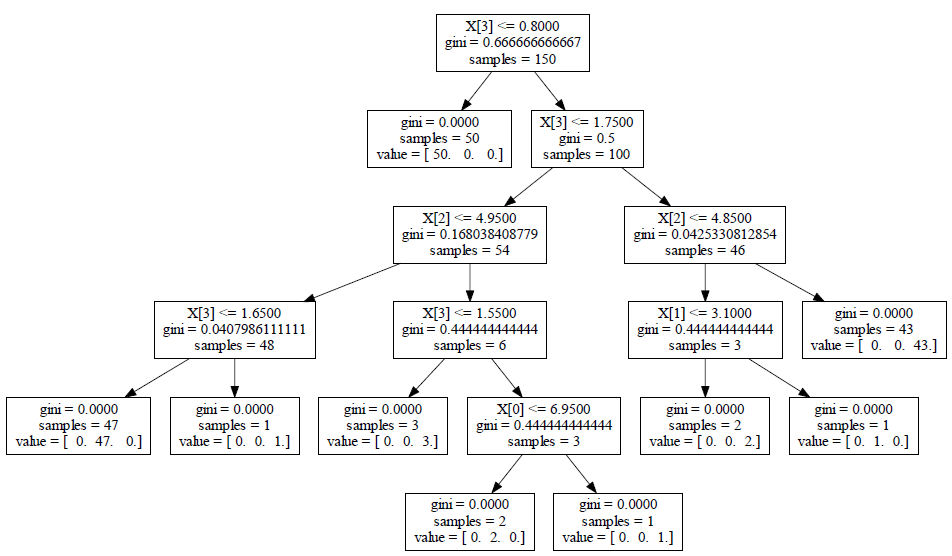
Uzyskane w powyższym przykładzie drzewo klasyfikacyjne ilustruje rysunek irisDT. Każdy węzeł drzewa prezentuje odpowiedni test dla atrybutu, wartość indeksu Giniego ze względu na ten test oraz liczbę próbek związanych z tym węzłem. W przypadku liścia prezentowana jest klasa mu odpowiadająca za pomocą macierzy value.

Rysunek 2: Drzewo klasyfikacyjne dla zbioru Iris. Źródło: opracowanie własne