Sztuczne sieci neuronowe

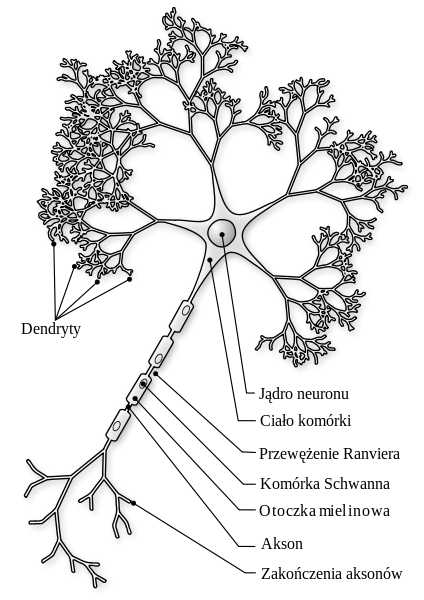
Sztuczne sieci neuronowe (por. [Stapor2005], [Stapor2011], [Tadeusiewicz1993], [Osowski2006], [Osowski2013], [Zurada1996]) swoje wzorce wywodzą z biologii i obserwacji ludzkich komórek nerwowych. Ludzki mózg posiada ok 100mld neuronów połączonych ze sobą. Są to proste struktury, podobne do siebie. Między neuronami jest ok \(10^{15}\) połączeń. Do każdego neuronu dochodzą pewne sygnały (bodźce). Takie impulsy mają częstotliwość \(1-100Hz\) i czas trwania \(1-2ms\). Impulsy są doprowadzane za pomocą synaps. Bodźce pochodzące od synaps wywoływane są przez specjalne substancje chemiczne, zwane neuromediatorami. Zmiana potencjału elektrycznego komórki zależna jest od ilości neuromediatora w synapsie. Sygnał wyjściowy jest wyprowadzany z komórki za pomocą aksonu. Sygnały wyjściowe neuronów mogą być sygnałami wejściowymi innych neuronów. Sygnałami pobudzającymi neurony mogą być także sygnały pochodzące z receptorów nerwowych. Szybkość pracy ludzkiego mózgu to ok \(10^{18}\) operacji na sekundę. Pierwszy model neuronu został zaproponowany w 1943 roku przez McCullocha i Pittsa (por. [McCulloch1943]). Był to prosty neuron, który mógł modelować funkcje logiczne takie jak OR lub AND. W roku 1949 Donald Hebb odkrył, że informacja może być przechowywana w strukturze połączeń między neuronami i zaproponował metodę uczenia sieci polegającą na zmianie wag. Jest to tak zwana reguła Hebba (por. [Hebb1949]). W 1958 roku Rosenblatt zaproponował model perceptronu (por. [Rosenblatt65]), a w roku 1960 powstały modele sieci Adaline i Madaline autorstwa Widrowa i Hoffa (por. [Widrow1960]). W roku 1969 w książce Perceptrons Minsky i Pappert wykazali, że reguły perceptronowe są użyteczne tylko dla pewnych zestawów danych. Było to powodem zahamowania na wiele lat rozwoju sieci neuronowych. W 1982 roku John Hopfield wprowadził sieć ze sprzężeniami zwrotnymi (por. [Hopfield1982]). Sieć służyła do odtwarzania obrazu z fragmentów oraz do rozwiązywania zadań optymalizacyjnych. Również w roku 1982r. Kohonen wprowadził samoorganizujące się sieci neuronowe (SOM) (por. [Kohonen1982]) do wydobywania cech.

../_images/neuron.png

Rysunek 1: Biologiczny model neuronu. Żródło: wikipedia.org

Na podstawie biologicznego modelu, Rosenblatt (por. [Rosenblatt65]) wprowadził model sztucznego neuronu zwany perceptronem. Na perceptron składają się wejścia, przez które wpływają sygnały zewnętrzne \(x_i\), wagi \(w_{ij}\), których wartości identyfikujemy z ważnością wejść, element sumujący, w którym obliczane jest łączna wartość pobudzenia \(u_j\) neuronu oraz funkcja aktywacji \(f\), której wartość determinuje stan wyjścia neuronu na podstawie pobudzenia. Przyjmujemy, że wejściem o numerze \(0\) wpływa sygnał stały \(x_0=1\). Temu sygnałowi odpowiada waga \(w_0\). Waga \(w_{ij}\) charakteryzuje połączenie skierowane od \(i\)-tego wejścia do \(j\)-tego neuronu. Sygnały dochodzące \((x_1, x_2, \ldots, x_N)\) do neuronu mnożone są przez \(w_{ij}\) otrzymując łączne pobudzenie neuronu

\[\begin{eqnarray} u_j(k)=\sum_{i=1}^Nw_{ij}x_i. \end{eqnarray}\]

jeśli funkcja aktywacji jest funkcją dyskretną to uzyskujemy tzw. perceptron dyskretny. Zazwyczaj przyjmuję się, że funkcja \(f\) jest funkcją różniczkowalną w swojej dziedzinie. W najprostszym przypadku może to być funkcja liniowa \(f(u)=u\). Stosowane są również funkcje nieliniowe takie jak np funkcja sigmoidalna. Charakteryzują się one tym, że odwzorowują wartości pobudzeń neuronu w ograniczony zakres wartości wyjść.

Na podstawie wag pochodzących od sygnałów obliczany jest stan wewnętrzny neuronu \(u_i\), natomiast odpowiedź neuronu \(y_i\) zależy od tego czy stan wewnętrzny neuronu (jego pobudzenie) przekracza pewien poziom. Odpowiada za to funkcja aktywacji \(f(u_i)\), która w modelu Rosenblatta jest bipolarną funkcją progową

\[\begin{split}\begin{eqnarray} f(u_i)=\left\{\begin{array}{lll} 1 & \textrm{ dla } & u_i>0\\ -1 & \textrm{ dla } & u_i\leq 0 \end{array}\right. \end{eqnarray}\end{split}\]
../_images/modelmp.JPG

Rysunek 2: Matematyczny model sztucznego neuronu Rosenblatta.

Najczęściej stosowanymi funkcjami aktywacji neuronu (oprócz funkcji liniowej) są unipolarną funkcją progową

\[\begin{split}\begin{eqnarray} f(u_i)=\left\{\begin{array}{lll} 1 & \textrm{ dla } & u_i>0\\ 0 & \textrm{ dla } & u_i\leq 0 \end{array}\right. \end{eqnarray}\end{split}\]

funkcja sigmoidalna unipolarna

(1)\[\begin{eqnarray} f(u_i)=\frac{1}{1+e^{-\beta x}} \end{eqnarray}\]

funkcja sigmoidalna bipolarna

\[\begin{eqnarray} f(u_i)=\frac{2}{1+e^{-\beta x}}-1 \end{eqnarray}\]

oraz tangens hiperboliczny.

\[\begin{eqnarray} f(u_i)=tanh(\beta u_i)=\frac{1-e^{\beta x}}{1+e^{-\beta x}} \end{eqnarray}\]

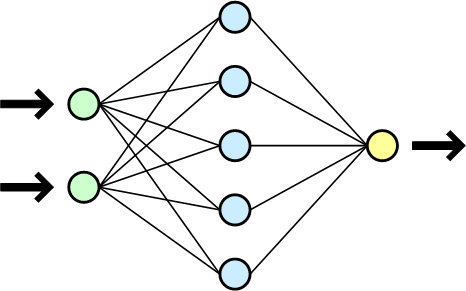
gdzie \(\beta\in[0,1]\). Sztuczną sieć neuronowa uzyskuje się łącząc ze sobą warstwy neuronów. Poniżej pokazano model sieci wielowarstwowej.

../_images/ssnwielowarstwowa.png

Rysunek 3: Model wielowarstwowej sztucznej sieci neuronowej. Żródło: wikipedia.org

Sygnały wyjściowe warstwy pierwszej są jednocześnie sygnałami wejściowymi neuronów warstwy drugiej, która jest jednocześnie warstwą wyjściową sieci. Odpowiedzi neuronów tej warstwy to odpowiedź całej sieci. Dodawanie do sieci nowych warstw zwiększa moc obliczeniową sieci. Dzięki wykorzystaniu wielu warstw, sieć potrafi rozwiązywać problemy, z którymi nie radzi sobie sieć jednowarstwowa np. problemy nieliniowe.

Uczenie sieci to dobór odpowiedniego zestawu wag dla danego zadania. Ogólnie uczenie sieci możemy podzielić na uczenie nie nadzorowane i nadzorowane. W metodzie uczenia pod nadzorem na podane na wejści sygnały \(x\) Sieć odpowiada sygnałami \(y\). Te sygnały to wyjścia poszczególnych neuronów. Wiedząc jakie sygnały są poprawne (oznaczmy je jako \(d\)) na wyjściu sieci dla każdego sygnału \(x\) możemy je porównać z aktualną odpowiedzią sieci, po czym w razie potrzeby zmodyfikować wagi neuronów. Dobór odpowiednich wag odpowiada procesowi minimalizacji funkcji błędu, którą można zapisać jako:

\[\begin{eqnarray} E=\sum_{i=1}^N\left(y_i(k)-d_i(k)\right)^2 \end{eqnarray}\]

Sumaryczny błąd uwzględniający wszystkie prezentowane sieci dane uczące można zapisać jako:

\[\begin{eqnarray} E=\sum_{i=1}^N\sum_{k=1}^p\left(y_i(k)-d_i(k)\right)^2 \end{eqnarray}\]

Błąd ten jest równy sumie błędów wszystkich neuronów (sumowanie po \(i\)) ze względu na wszystkie prezentowane im dane uczące (sumowanie po \(k\)). Modyfikacja wag odbywa się według wzoru:

\[\begin{eqnarray} w_{ij}(k+1)=w){ij}(k)+\Delta w_{ij}(k) \end{eqnarray}\]

gdzie \(i\) oznacza numer neuronu, \(j\) oznacza kolejną wagę tego neuronu, a \(k\) oznacza krok czasowy. Konkretna wartość \(\Delta w_{ij}\) zależy od przyjętego algorytmu uczenia. Do uczenia sieci często używa się metod gradientowych – obliczając gradient funkcji błędu a następnie modyfikując wartości wag w kierunku największego spadku funkcji błędu. Do doboru wartości wag wykorzystuje się również algorytmy genetyczne.

Niektóre rodzaje sieci neuronowych uczone tzw. metodą uczenie bez nadzoru. To znaczy, uczenie przebiega bez wykorzystania zbioru wzorcowych odpowiedzi (wektora poprawnej klasyfikacji w zdaniu klasyfikacji danych). Sieć uczona jest za pomocą jedynie danych wejściowych. Taka metoda uczenia jest wykorzystywana np. w sieci Hebba czy Kohonena, które z kolei wykorzystuje się min. w zadaniach klasteryzacji (grupowania).

Następna część - Podstawowe modele sieci neuronowych