Podstawowe modele sieci neuronowych¶

Perceptron¶

Model McCullocha-Pittsa przedstawiony na rysunku 2 jest punktem wyjścia do konstrukcji najprostszej sztucznej sieci neuronowej o nazwie perceptron (zwanej również perceptronem Rosenblatta, por. [Stapor2005], [Stapor2011], [Tadeusiewicz1993], [Osowski2006], [Osowski2013], [Zurada1996]. Zadaniem perceptronu jest klasyfikacja podanego na wejście wektora \(x\) do jednej z dwóch klas \(C_1\) lub \(C_2\). Jeśli sygnał wyjściowy neuronu przyjmuje wartość \(1\) to wektor \(x\) jest zaklasyfikowany do klasy \(C_1\), jeśli przyjmuje wartość \(0\) to do klasy \(C_2\). Perceptron dzieli \(N\)-wymiarową przestrzeń wektorów wejściowych na dwie półprzestrzenie rozdzielone \(N-1\) wymiarową hiperpłaszczyzną. Hiperpłaszczyzna ta zwana jest granicą decyzyjną. Jeśli przestrzeń obiektów jest dwuwymiarowa to rozdzielająca je granica jest linią prostą.

Reguła uczenia perceptronu¶

Uczenie perceptronu polega na znalezieniu wartości jego wag. Różnica pomiędzy oczekiwaną wartością wyjścia neuronu a wartością otrzymaną stanowi błąd popełniony przez neuron przy prezentacji j-tego przykładu:

(1)\[\begin{eqnarray}\label{deltaperceptron} \delta_j=d_j-y_j \end{eqnarray}\]

Naszym celem jest znalezienie takie rozwiązania, które minimalizuje następującą perceptronową funkcję kryterialną

(2)\[\begin{eqnarray}\label{jodw} J(\tilde{w})=\sum_{x_i, d_i(w^Tx+w_0}(-\tilde{w}^tx-\tilde{w}_0) \end{eqnarray}\]

W powyższej funkcji kryterialnej sumowanie odbywa się po obiektach niepoprawnie zaklasyfikowanych, co prowadzi do minimalizacji liczby niepoprawnych zaklasyfikowań. W praktyce często stosuje się równoważny zapis

\[\begin{eqnarray} J(\tilde{w})=\sum_{x_i, d_i(w^Tx+w_0}(-\tilde{w}^tx) \end{eqnarray}\]

gdzie \(x=[1,x_1, x_2, ..., x_N]^T\). Poszukiwanie minimum perceptronowej funkcji kryterialnej jest równoważne minimalizacji błędu średniokwadratowego

\[\begin{eqnarray} Q=\frac{1}{2}\sum_{j=1}^N(d_j-y_j)^2=\sum_{j=1}^N Q_j^2,\quad Q_j=\frac{1}{2}\delta_j^2 \end{eqnarray}\]

gdzie \(\delta\) jest dana wzorem (1). Minimum powyższej funkcji kryterialnej poszukujemy metodą największego spadku gradientu

Przykład 22

Rozważmy następujący problem klasyfikacyjny. Zbiór uczący składa się z czterech obiektów \([[0, 0], [0, 1], [1, 0], [1, 1]]\), których poprawna klasyfikacja to \([[0], [0], [0], [1]]\). Zbiór testowy również składa się z czterech obiektów \([[2, 1], [2,2], [-1,0], [-1,1]]\), których poprawna klasyfikacja to \([[1], [1], [0], [0]]\). Wykorzystując jednowarstwowy perceptron dokonujemy klasyfikacji zbioru testowego. Uczenie perceptronu zgodnie z regułą delta. Obliczony średni błąd kwadratowy wynosi \(0\). Wszystkie obiekty zbioru testowego zostały poprawnie zaklasyfikowane. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę.

import neurolab as nl
import numpy as np
import pylab as pl

#Zbiór uczący
train = [[0, 0], [0, 1], [1, 0], [1, 1]]
train_target = [[0], [0], [0], [1]]

#Zbiór testowy
test = [[2, 1], [2,2], [-1,0], [-1,1]]
test_targets=[[1], [1], [0], [0]]

#Tworzymy sieć z 2 wejściami i 1 neuronem
net = nl.net.newp([[-1, 2],[0, 2]], 1)

#Uczymy sieć
error = net.train(train, train_target, epochs=100, show=10, lr=0.1)

#Symulujemy
out = net.sim(test)

#Obliczamy błąd
f = nl.error.MSE()
test_error = f(test_targets, out)

print "Błąd klasyfikacji: %f" %test_error

Metoda największego spadku gradientu¶

Metoda największego spadku gradientu to jedna z podstawowych meto uczenia sieci neuronowych (por. [Stapor2005], [Stapor2011], [Tadeusiewicz1993], [Osowski2006], [Osowski2013], [Zurada1996]) . Rozpoczynając od rozwiązania losowego w każdym kroku uczenia do aktualnych wartości wag dodaje się poprawkę wprost proporcjonalną do gradientu funkcji kryterialnej w punkcie w (aktualna wartość wag) według wzoru:

\[\begin{eqnarray} w_{k+1} = w_{k} - \eta \nabla\left(J(w_k)\right) \end{eqnarray}\]

Gradient funkcji \(J(w)\) danej wzorem (2) jest równy

\[\begin{eqnarray} \nabla J=\sum_{x_i, d_i(w^Tx+w_0}(-x) \end{eqnarray}\]

Powyższy algorytm prezentujemy na poniższym schemacie.

Algorytm 21 Metoda największego spadku gradientu

Dane: \(X_{train}\) - zbiór uczący

Wyniki:\(w\) - zestaw wag

Inicjuj wagi perceptronu wartościami losowymi
Podaj kolejny j-ty wektor zbioru uczącego i oblicz odpowiedź perceptronu
Jeżeli \(d_j\neq y_j\) zmodyfikuj wagi neuronu, według wzoru
\(w_{k+1}=w_k+\eta d_jx_j\)
Jeżeli \(j=N\) oblicz błąd całej epoki i w przypadku gdy jest większy od założonej wartości podstaw \(j=1\) i idź do 2.

Posługując się metodą największego spadku gradientu dostajemy zależność pomiędzy modyfikacją i-tej wagi neuronu a zmianą wartości błędu przezeń popełnianego przy prezentacji j-tego przykładu.

Twierdzenie 7

Jeżeli istnieje wektor wag \(w\) oraz stała \(w_0\) takie, że dla każdego obiektu zbioru uczącego zachodzi \(d_i(w^Tx+w_0)>0\), to algorytm uczenia perceptronu pozwala na odnajdzie wag \(w\) oraz \(w_0\) w skończonej liczbie kroków dla dowolnych wartości wag początkowych.

Dla uczenia perceptronu stosować można również następujący algorytm uczenia kieszonkowego\

Algorytm 22 Metoda największego spadku gradientu

Dane: \(X_{train}\) - zbiór uczący

Wyniki:\(w\) - zestaw wag

Wagi \(w_0\) perceptronu inicjuj wartościami losowymi i zapisz je w kieszonce jako rekordzistę z zerowym czasem życia, ustaw numer iteracji na wartość 0.
Losuj wektor zbioru uczącego i oblicz odpowiedź perceptronu
Jeżeli \(d_j\neq y_j\) to zmodyfikuj wagi neuronu, według wzoru \(w_{k+1}=w_k+\eta d_jx_j\).
W przeciwnym wypadku zwiększ czas życia zestawu wag o 1.
Jeśli czas życia zestawu wag jest większy niż u rekordzisty zapominamy starego rekordzistę i zapisujemy w kieszonce nowy układ wag.
Jeżeli przekroczona została liczba iteracji zakończ algorytm, w przeciwnym wypadku wróć do kroku 2.

Perceptron wielowarstwowy¶

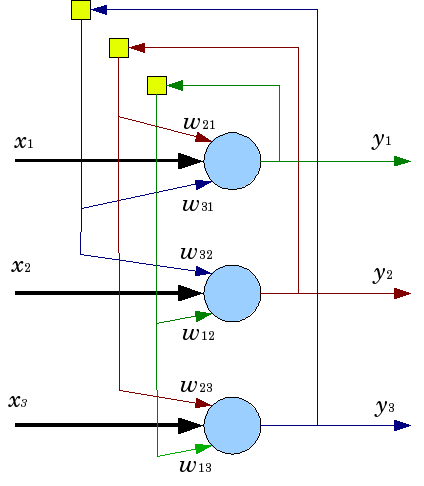
Wielowarstowy perceptron (MLP) (por. [Stapor2005], [Stapor2011], [Tadeusiewicz1993]) jest oparty o opisany powyżej pojedyńczy pereptron. Sieć ta składa się z wielu warstw pojedynczych neuronów, w ten sposób, że wyjścia neuronów warstwy poprzedniej tworzą wektor podawany na wejście każdego z neuronów warstwy następnej. Neurony każdej warstwy mają zawsze tę samą liczbę wejść równą liczbie neuronów warstwy poprzedniej + 1, natomiast w ramach jednej warstwy neurony nie mają połączeń między sobą. Schemat budowy wielowarstwowego perceptronu przedstawia poniższy rysunek.

Rysunek 4: Model wielowarstwowego perceptronu. Źródło: wikipedia.org

Na rysunku 4 pokazany jest schemat 3-warstwowego preceptronu o architekturze \(d-M-c\). Ta sieć neuronowa nie ma sprzężeń zwrotnych tzn wszystkie neurony ustawione są w jednym kierunku od wejść do wyjść sieci. Pierwsza warstwa to warstwa wejściowa mogąca za zadanie przechwycenie sygnału i przekazanie go do kolejnych warstw sieci (zwanych warstwami ukrytymi). Zazwyczaj modele sieci neuronowych posiadają jedną warstwę ukrytą. Ostatnia warstw sieci to warstwa wyjściowa, w której neuronach formowane są sygnały wyjściowe. Sieć z rysunku 4 ma \(d\) wejść, \(M\) neuronów w jednej warstwie ukrytej oraz \(c\) neuronów w warstwie wyjściowej. W ogólnym przypadku liczba wejść w sieci wyznaczona jest przez wymiar przestrzeni cech, natomiast liczba neuronów w warstwie wyjściowej najczęściej równa jest liczbie klas.

Rozważmy następujące zadanie klasyfikacji. Załóżmy, że \(x=[X_1,\ldots,x_p]\) będzie klasyfikowanym obiektem. Wektor ten rozszerzony o dodatkową składową równą 1 jest podawany na wejście sieci, w związku z tym warstwa wejściowa klasyfikatora neuronowego liczy p+1 neuronów. Warstwa wyjściowa liczy \(L\) neuronów gdzie \(L\) jest liczbą klas. Odpowiedzą sieci jest wektor

\[\begin{eqnarray} y=[y_1,\ldots, y_N] \end{eqnarray}\]

Funkcje klasyfikujące klasyfikatora neuronowego postaci

\[\begin{eqnarray} g_j(x)=y_j \quad\textrm{ dla } j=1,\ldots, L \end{eqnarray}\]

interpretujemy je jako miarę przynależności do klas Proces uczenia odbywa się na podstawie informacji ze zbioru uczącego. W jego trakcie modyfikowane są wagi poszczególnych neuronów. W klasyfikatorze neuronowym najczęściej wykorzystywaną funkcją aktywacji jest unipolarna funkcja sigmoidalna (?). Przy założeniu, że funkcja aktywacji jest ciągłą można wykorzystać metodę największego spadku gradientu do minimalizacji funkcji celu

\[\begin{eqnarray} E=\frac{1}{2}\sum_{k=1}^p\sum_{i=1}^M(y_i^k-d_i^k)^2 \end{eqnarray}\]

Adaptacja wag odbywa się wg. wzoru

\[\begin{eqnarray} w_{k+1}=w_k+\Delta w \end{eqnarray}\]

gdzie \(\Delta w=\eta p(w)\). Modyfikowane są wagi pojedynczych neuronów sieci tak, że nowy wektor wag neuronu wyznaczany jest ze wzoru:

\[\begin{eqnarray} w_{k+1}=w_k+\eta\delta x \end{eqnarray}\]

gdzie \(x\) jest wektorem podanym na wejście neuronu rozszerzonym o dodatkową składową równą 1, \(\eta\) jest współczynnikiem liczbowym decydującym o szybkości uczenia, \(\delta\) jest różnica między oczekiwaną wartością odpowiedzi sieci, a wartością rzeczywistą y pomnożoną przez wartość pochodnej funkcji aktywacji. Aby zmodyfikować wagi neuronu trzeba znać oczekiwaną wartość odpowiedzi dla neuronu, która to wartość jest znana tylko w przypadku neuronów warstwy wyjściowej.

Algorytm wstecznej propagacji błędów¶

W przypadku sieci wielowarstwowych najczęściej stosowanym algorytmem uczenia jest algorytm wstecznej propagacji błędów (por. [Stapor2005], [Stapor2011], [Tadeusiewicz1993], [Osowski2006], [Osowski2013], [Zurada1996]). Jego nazwa pochodzi stąd, iż po obliczeniu odpowiedzi sieci na zadany wzorzec, obliczana jest wartość gradientu funkcji błędu dla neuronów ostatniej warstwy. Następnie modyfikuje się ich wagi. Błąd jest propagowany do warstwy wcześniejszej (przedostatniej). Wartości funkcji gradientu dla neuronów z tej warstwy obliczane są w oparciu o gradienty dla neuronów z warstwy następnej (czyli ostatniej). Modyfikowane są wagi kolejnej warstwy. Postępowanie trwa aż do warstwy wejściowej. Otrzymuje się zatem wzór opisujący składowe wektora \(\delta\)

\[\begin{eqnarray} \delta_{(i,n)}=\left(\sum_{k}\delta_{i+1,k)}w_{(k,n)}\right)y_n(1-y_n) \end{eqnarray}\]

gdzie indeks \(i\) oznacza numer warstwy (\(i\) – aktualna, \(i+1\) - następna), \(k\) numer neuronu w warstwie następnej, \(n\) numer aktualnie rozpatrywanego neuronu (n-ta składowa wektora wejściowego dla następnej warstwy).

Algorytm 23 Algorytm wstecznej propagacji błędów

Dane: \(X_{train}\) - zbiór uczący

Wyniki:\(w\) - zestaw wag

Podanie na wejście wektora uczącego x i obliczenie aktualnego wyjścia y
Obliczenie błędów w warstwie ostatniej na podstawie różnicy otrzymanych wartości wektora y oraz wzorcowych d
Adaptacja wag od warstwy wejściowej do wyjściowej
Obliczenie błędów dla neuronów we wszystkich warstwach wcześniejszych po kolei (jako funkcji błędu warstwy następnej, który jest już znany)
Powtarzamy procedurę do momentu kiedy sygnały wyjściowe sieci będą dostatecznie bliskie oczekiwanym

Istnieje wiele wariantów i ulepszeń oryginalnej metody wstecznej propagacji błędów. Pozwalają one uzyskać lepsze efekty uczenia lub przyśpieszyć proces nauki.

Przykład 23

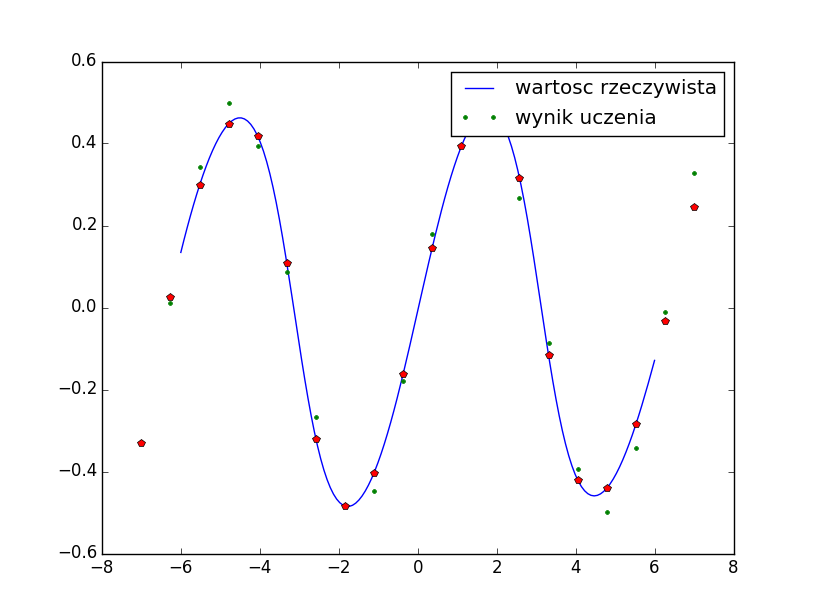
Rozważmy zadanie aproksymacji funkcji \(f(x)=\frac{1}{2}\sin{x}\). W tym celu wykorzystamy wielowarstwowy perceptron składający się z 2 warstw. Początkowe wartości wag będą generowane w sposób losowy. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę oraz wykres przedstawiający rzeczywiste wartości funkcji \(f(x)=\frac{1}{2}\sin{x}\) oraz te oszacowane za pomocą sieci MLP (rys 5).

import neurolab as nl
import numpy as np
import pylab as pl

#Tworzymy zbiór ucząc
x = np.linspace(-7, 7, 20)
y = np.sin(x) * 0.5

size = len(x)
print x
inp = x.reshape(size,1)
print inp
tar = y.reshape(size,1)

#Tworzymy sieć z dwoma warstwami, inicjalizowaną w sposób losowy,
#w pierwszej warstwie 5 neuronów, w drugiej warstwie 1 neuron
net = nl.net.newff([[-7, 7]],[5, 1])

#Uczymy sieć, wykorzystujemy metodę największego spadku gradientu
net.trainf = nl.train.train_gd
error = net.train(inp, tar, epochs=500, show=100, goal=0.02)

#Symulujemy
out = net.sim(inp)

#Tworzymy wykres z wynikami
x2 = np.linspace(-6.0,6.0,150)
y2 = net.sim(x2.reshape(x2.size,1)).reshape(x2.size)
y3 = out.reshape(size)

pl.plot(x2, y2, '-',x , y, '.', x, y3, 'p')
pl.legend(['wartosc rzeczywista', 'wynik uczenia'])
pl.show()

Rysunek 5: Aproksymacja wartości funkcji \(f(x)=\frac{1}{2}\sin{x}\) za pomocą MLP [opr. własne].

Siec Hopfielda¶

Sieć Hopfielda , (por. [Tadeusiewicz1993], [Osowski2013], [Zurada1996]) znana jako sieć asocjacyjna to w przeciwieństwie do poprzednio omawianych sieci sieć rekurencyjna. Sieć Hopfielda została wprowadzona przez amerykańskiego fizyka Johna Hopfielda w 1982 roku (por. [Hopfield1982]). Są wykorzystywane do modelowania pamięci skojarzeniowej. Taka sieć dają możliwość rekonstrukcji i rozpoznawania wcześniej zapamiętanych wzorców na podstawie skojarzeń, bazując na dostępnym fragmencie wzorca lub wzorca podobnego do niego. Strukturę sieci Hopfielda można opisać jako układ wielu identycvznych elementów połączonych ze sobą każdy z każdym. Sieć Hopfielda jest najczęściej rozpatrywana jako struktura jednowarstwowa. W odróżnieniu od sieci warstwowych typu perceptron sieć Hopfielda jest siecią rekurencyjną, gdzie neurony są wielokrotnie pobudzane w jednym cyklu rozpoznawania co uzyskuje się poprzez pętle sprzężenia zwrotnego.

Rysunek 6: Jednowarstwowa sieć Hopfielda ze sprzężeniem zwrotnym. Żródło: wikipedia.org

Wagi połączeń wyliczane są w sieci Hopfielda a priori, jej faza uczenia ogranicza się do wyliczenia wartości wag zgodnie z zasadą uczenia Hebba

\[\begin{split}w_{ij}=\left\{\begin{array}{ll} \sum_{k=1}^Mx_i^kx_j^k & \textrm{ dla } i\neq j\\ 0 & \textrm{ dla } i=j \end{array}\right.\end{split}\]

gdzie \(M\) jest ogólną liczbą zapamiętywanych wzorców, \(x_i\in\{-1, 1\}\) to i-ta składowa wzorca, natomiast górny indeks określa numer wzorca. W fazie odtwarzania na wejście sieci podany jest nieznany sygnał wejściowy i zadaniem sieci jest w procedurze rekurencyjnej „znaleźć” ten z zapisanych w jej strukturze wzorców do którego ten sygnał wejściowy jest najbardziej podobny.

Przykład 24

Rozważmy zadanie rozpoznawania pisma. Jako zbiór uczący przyjmujemy macierz określającą litery N, E, R, O. każda litera jest reprezentowana prze 25-cio wymiarowy wektor, których składowe reprezentują piksele 0-biały, 1-czarny. Zbiorem testowym jest natomiast zniekształcona litera N. W tym zadaniu wykorzystamy sieć Hopfielda. Sieć poprawnie rozpoznaje wszystkie elementy zbioru uczącego. Różnież zniekształcona litera N została poprawnie rozpoznana w drugiej interacji sieci. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę.

import numpy as np
import neurolab as nl

#Zbiór danych wejściowych to litery: N, E, R, O.
#Każda z liter jest zapisywana w macierzy 5x5
target =  [[1,0,0,0,1,
           1,1,0,0,1,
           1,0,1,0,1,
           1,0,0,1,1,
           1,0,0,0,1],
          [1,1,1,1,1,
           1,0,0,0,0,
           1,1,1,1,1,
           1,0,0,0,0,
           1,1,1,1,1],
          [1,1,1,1,0,
           1,0,0,0,1,
           1,1,1,1,0,
           1,0,0,1,0,
           1,0,0,0,1],
          [0,1,1,1,0,
           1,0,0,0,1,
           1,0,0,0,1,
           1,0,0,0,1,
           0,1,1,1,0]]

chars = ['N', 'E', 'R', 'O']
target = np.asfarray(target)
target[target == 0] = -1

#Tworzymy i testujemy sieć Hopfielda
net = nl.net.newhop(target)

#Symulujemy dla elementów zbioru uczącego
output = net.sim(target)
for i in range(len(target)):
    print(chars[i], (output[i] == target[i]).all())

#Symulujemy dla zniekształconej litery N
test =np.asfarray([0,0,0,0,0,
                   1,1,0,0,1,
                   1,1,0,0,1,
                   1,0,1,1,1,
                   0,0,0,1,1])
test[test==0] = -1
out = net.sim([test])
print ((out[0] == target[0]).all(), 'Liczba krokow'
       ,len(net.layers[0].outs))

Samoorganizujące się sieci Kohonena¶

Sieci Kohonena (zwane też SOM – Self Orgenizing Maps, por. [Tadeusiewicz1993], [Osowski2013], [Zurada1996]) są przykładem sieci uczonych bez nadzoru. Neurony w sieci Kohonena są uporządkowane względem siebie przestrzennie np. za pomocą siatki dwuwymiarowej. Przykładowa sięc Kohonena została pokazana na rysunku 7.

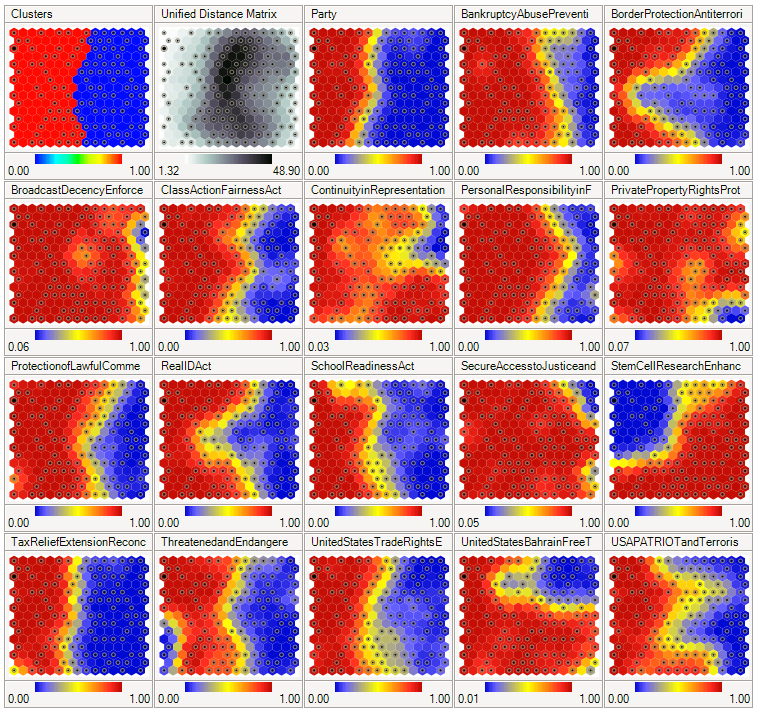
Rysunek 7: Sieć Kohonena pokazująca wzorce głosowania w kongresie USA. Pierwsze dwa rysunki pokazują wzorce i odległość, natomiast kolejne obrazują płaszczyzny komponentów. Czerwony kolor oznacza głosowanie na tak, niebieski głosowanie na nie. Żródło: wikipedia.org

W sieci Kohonena mówimy o sąsiedztwie danego neuronu. Sąsiedztwo neuronu to inne neurony leżące blisko danego neuronu w przestrzeni wyznaczonej przez zastosowane uporządkowanie neuronów. Uczenie polega na wyznaczeniu zwycięskiego neuronu i modyfikacji jego wektora wag w kierunku prezentowanego wektora wejściowego \(x\). Zwycięskim neuronem jest ten neuron, którego wagi są najbardziej zbliżone do prezentowanego wektora danych wejściowych. Zatem wektor wag zwycięskiego neuronu wyznacza się za pomocą

\[\begin{eqnarray} d(x,w_w)=\min_{1\leq i\leq n} d(x,w_i) \end{eqnarray}\]

Norma \(d\) może by dowolną normą (np. euklidesową). W trakcie uczenia sieci zwycięzca oraz jego sąsiedztwo podlega adaptacji wag zgodnie z następującą regułą Kohonena

\[\begin{eqnarray} w_i(k+1)=w_i(k)+\eta_i(k)[x-w_i(k)] \end{eqnarray}\]

Parametr \(\eta\) to krok uczenia, przeważnie malejący w trakcie kolejnych iteracji. W przypadku danych wejściowych o małych wymiarach istnieje potrzeba normalizacji wektorów wejściowych.

Współczynniki uczenia maleją wraz z odległością od zwycięzcy, natomiast wagi neuronów spoza sąsiedztwa nie podlegają zmianom. Algorytm uczenia sieci neuronowej (nazywany również algorytmem algorytmem WTM – Winner Takes Most) można zapisać jako

\[\begin{eqnarray} w_i(k+1)=w_i(k)+\eta_i(k)G(i,x)[x-w_i(k)] \end{eqnarray}\]

gdzie \(G(i,x)\) jest funkcją sąsiedztwa. W klasycznym algorytmie Kohonena funkcja \(G(i,x)\) zdefiniowana jest jako:

\[\begin{split}\begin{eqnarray} G(i,x)=\left\{\begin{array}{lll} 1 & \textrm{ dla } & d(i,w)\leq\lambda\\ 0 & \textrm{ dla } & d(i,w)>\lambda \end{array}\right. \end{eqnarray}\end{split}\]

gdzie \(d(i,w)\) jest odległością pomiędzy neuronami w przestrzeni sieci tzn. na siatce (a nie w przestrzeni danych wejściowych!), a lambda jest promieniem sąsiedztwa malejącym do zera w trakcie nauki. Jest to tzw. sąsiedztwo prostokątne. Innym rodzajem sąsiedztwa jest sąsiedztwo gaussowskie:

\[\begin{eqnarray} G(i,x)=exp\left( -\frac{d^2(i,w)}{2\lambda^2}\right) \end{eqnarray}\]

W tym przypadku stopień aktywacji neuronów jest zróżnicowany w zależności od wartości funkcji Gaussa. Sąsiedzi neuronu zwycięskiego są modyfikowani w różnym stopniu. Często stosowanym podejściem jest wyróżnienie dwóch faz uczenia sieci Kohonena:

wstępną (ang. ordering phase), podczas której modyfikacji ulegają wagi neuronu zwycięzcy oraz jego sąsiedztwa malejącego z czasem
końcową (ang. convergence phase), podczas której modyfikowane są wagi jedynie neuronu zwycięzcy.

Mają one na celu najpierw wstępne nauczenie sieci, a następnie jej dostrojenie.

Zastosowanie sieci Kohonena:

wykrywanie związków w zbiorze wektorów
uczenie się rozkładu danych
kompresja obrazów
wykrywanie nieprawidłowości

Przykład 25

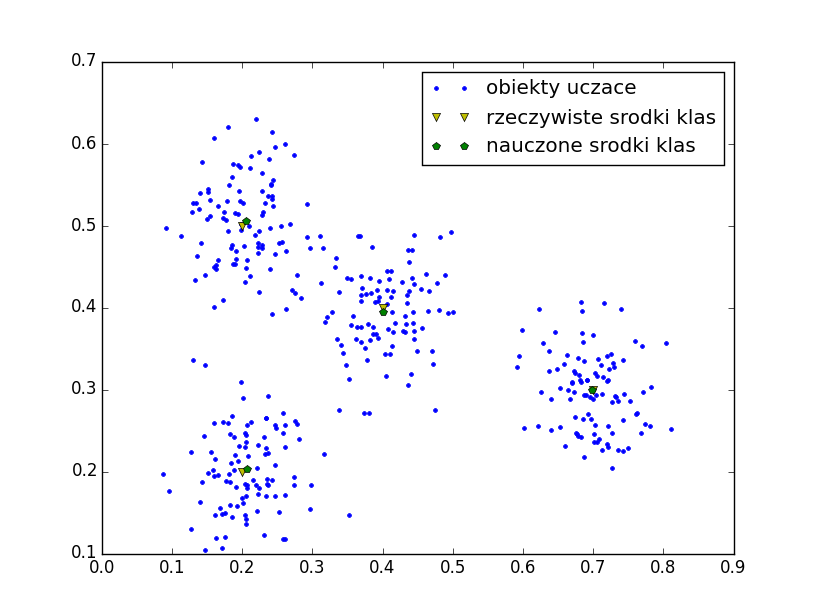
Rozważmy zadanie wyznaczenia środków klas. W tym celu wykorzystamy sieć Kohonena. Elementy zbioru uczącego zostały wygenerowane z rozkładu normalnego. Sieć Kohonena składa się z dwóch wejść i 4 neuronów. Jako algorytm uczenia wykorzystujemy algorytm Winner Takes All. Poniżej prezentujemy skrypt w języku python realizujący powyższą procedurę oraz wykres przedstawiający rzeczywiste środki klas oraz wartości oszacowane za pomocą sieci Kohonena (rys 8).

import numpy as np
import neurolab as nl
import numpy.random as rand
import pylab as pl

#Tworzymy zbiór danych
#Środki klas
centr = np.array([[0.2, 0.2], [0.4, 0.4], [0.7, 0.3], [0.2, 0.5]])
rand_norm = 0.05 * rand.randn(100, 4, 2)
#dane uczące
inp = np.array([centr + r for r in rand_norm])
inp.shape = (100 * 4, 2)
rand.shuffle(inp)

#Tworzymy sieć Kohonena z dwoma wejściami i 4 neuronami
net = nl.net.newc([[0.0, 1.0],[0.0, 1.0]], 4)
#Uczymy sieć zgodnie z algortmem Winner Take All
error = net.train(inp, epochs=200, show=20)

#Wyniki umieszczamy na wykresie:
w = net.layers[0].np['w']
pl.plot(inp[:,0], inp[:,1], '.', \
        centr[:,0], centr[:, 1] , 'yv', \
        w[:,0], w[:,1], 'p')
pl.legend(['obiekty uczace', 'rzeczywiste srodki klas',
           'nauczone srodki klas'])
pl.show()

Rysunek 8: Oszacowanie środków klas za pomocą sieci Kohonena [opr. własne].

Następna część - Test do rozdziału