Walidacja uczenia nienadzorowanego¶

Kryteria zewnętrzne oceny grupowania¶

Kryteria zewnętrzne stosujemy dla porównania wyniku grupowania z pewną założoną strukturą, to znaczy z innym podziałem tego zbioru. Dokonujemy tego przy użyciu pewnej miary porównania zgodności dwóch podziałów, którą nazywamy indeksem walidacyjnym. Przykłady takich miar, występujących w literaturze przedstawiamy poniżej, wprowadzając wcześniej pewne oznaczenia. Rozważmy dwa podziały zbioru uczącego na grupy \({{C}_{1}},...,{{C}_{K}}\) oraz \({{E}_{1}},...,{{E}_{S}}\). Niech \(N_{ij}\) oznacza liczbę obiektów należących zarówno do grupy \(C_i\) w pierwszym z podziałów oraz \(E_j\) w drugim z nich, zatem:

oraz niech:

Macierz rozmiaru \(K\times S\) złożoną z elementów \(N_{ij}\) nazywać będziemy macierzą konfuzji. Przyjęte oznaczenia pozwalają na wprowadzenie występujących najczęściej w literaturze zewnętrznych indeksów walidacyjnych:

1. Statystyka Randa [Rand1971]

   \[Rand=1+\left( \sum\limits_{i=1}^{K}{\sum\limits_{j=1}^{S}{N_{ij}^{2}}-\frac{1}{2}\left( \sum\limits_{i=1}^{K}{N_{i\cdot }^{2}}+\sum\limits_{j=1}^{S}{N_{\cdot j}^{2}} \right)} \right)\cdot \frac{2}{N\left( N-1 \right)}\]

2. Indeks Jaccarda [Jain1998]

   \[Jaccard=\frac{\sum\limits_{i=1}^{K}{\sum\limits_{j=1}^{S}{N_{ij}^{2}}-N}}{\sum\limits_{i=1}^{K}{N_{i\cdot }^{2}}+\sum\limits_{j=1}^{S}{N_{\cdot j}^{2}}-\sum\limits_{i=1}^{K}{\sum\limits_{j=1}^{S}{N_{ij}^{2}}-N}}\]

3. Indeks Fowlkesa-Mallowsa [Fowlkes1983]

   \[FM=\frac{\sum\limits_{i=1}^{K}{\sum\limits_{j=1}^{S}{N_{ij}^{2}}-N}}{2\sqrt{\sum\limits_{i=1}^{K}{\frac{N_{i\cdot }^{2}-{{N}_{i\cdot }}}{2}}\cdot \sum\limits_{j=1}^{S}{\frac{N_{\cdot j}^{2}-{{N}_{\cdot j}}}{2}}}}\]

4. Statystyka \(\Gamma\) Huberta [Hubert1985]

   \[\Gamma =\frac{2}{N\left( N-1 \right)}\sum\limits_{i=1}^{N-1}{\sum\limits_{j=i+1}^{N}{{{D}_{1}}\left( i,j \right){{D}_{2}}\left( i,j \right)}},\]

   gdzie \({{D}_{1}},{{D}_{2}}\) są macierzami sąsiedztwa dla porównywanych podziałów

Udowodniono że wartości powyższych indeksów rosną wraz ze wzrostem podobieństwa pomiędzy obydwa rozważanymi podziałami.

Kryteria wewnętrzne oceny grupowania¶

Ocena wewnętrzna grupowania polega na zweryfikowaniu hipotezy zerowej, mówiącej o braku struktury w zbiorze uczącym, wobec hipotezy alternatywnej mówiącej o możliwości zidentyfikowania w tym zbiorze grup obiektów podobnych. Zaproponowano wiele metod weryfikacji wspomnianej hipotezy na podstawie użytej statystyki testowej, która jest na ogół miarą rozrzutu wewnątrz-klasowego, bądź między-klasowego. W zależności od użytego algorytmu grupowania stosujemy odpowiednie kryteria oceny wewnętrznej do oceny hierarchii podziałów w przypadku algorytmów hierarchicznych, lub do konkretnego podziału uzyskanego w wyniku algorytmu podziałowego. W przypadku walidacji hierarchii podziałów rozważamy macierz sąsiedztwa dla obiektów zbioru uczącego, której elementy oznaczają poziom, na którym rozpatrywane obiekty po raz pierwszy zostają umieszczone w jednej grupie. W oparciu o taką macierz, którą oznaczamy \(CM\), od ang. cophenetic matrix, definiujemy miarę oceny pomiędzy macierzą \(CM\) a macierzą sąsiedztwa (odległości) \(D\), obliczoną dla tego zbioru danych. Zakładając, że macierz \(CM\) składa się z elementów \(c_{ij}\), natomiast macierz \(D\) z elementów \({{d}_{ij}}=d\left( {{x}_{i}},{{x}_{j}} \right)\), wspomniany indeks jest postaci [Farris1969] :

\({{\mu }_{D}},{{\mu }_{CM}}\) są średnimi z elementów macierzy \(D\) i \(CM\) odpowiednio, czyli:

Bliska zeru wartość powyższego indeksu oznacza wysokie podobieństwo macierzy \(D\) oraz \(CM\).

W przypadku walidacji konkretnego podziału, zadaniem jest zbadanie podobieństwa pomiędzy macierzą sąsiedztwa wyznaczoną przez odległości w zbiorze uczącym, a macierzą sąsiedztwa wyznaczoną przez podział otrzymany w efekcie grupowania. W tym przypadku również wykorzystać możemy statystykę \(\Gamma\) Huberta.

Inną miarą oceny wewnętrznej, możliwą do wykorzystania przy walidacji liczby grup, jest zaproponowana w [Tibshirani2001] statystyka oparta na mierze dyspersji wewnątrzgrupowej. Zakładając, że dany jest podział obiektów zbioru \(V\) na grupy \({{C}_{1}},...,{{C}_{K}}\) za miarę dyspersji wewnątrzgrupowej grupy \(k\) uważamy wielkość:

Metoda ta porównuje powyższą wartość z szacowaną metodą Monte-Carlo w \(B\) iteracjach wartością \(W_{k}^{b}\), (gdzie \(b\) jest numerem iteracji), przy założeniu prawdziwości hipotezy o braku więcej niż jednej grupy w rozważanym zbiorze danych. Hipoteza ta jest weryfikowana w ten sposób, że zakłada się że dane zbioru uczącego pochodzą z rozkładu jednostajnego. Zbiory z tego rozkładu są więc losowo generowane metodami Monte-Carlo. Statystyka Gap dla ustalonej liczby \(k\) grup wyraża się wzorem:

gdzie \(\mathop{\rm tr}\left( W \right)\) oznacza ślad macierzy \(W\). Wartości powyższej statystyki są liczone w pewnym zakresie liczby grup, a za najlepszy możliwy podział wśród podziałów na \(2,...,K\) grup uważany jest ten, który maksymalizuje wartość powyższego wyrażenia.

Kryteria względne oceny grupowania¶

Załóżmy, że poszukujemy optymalnej liczby grup \(K\), dającej w wyniku podział \({{C}_{1}},...,{{C}_{K}}\). W literaturze, np. w [Jain1998] istnieje cały szereg indeksów walidacyjnych omawianej grupy, w tym miejscu przedstawiamy kilka z częściej stosowanych.

1. Indeks Dunna:

   \[\begin{split}Dunn\left( K \right)=\underset{1\le i\le K}{\mathop{\rm min}}\,\left\{ \underset{\begin{smallmatrix} 1\le j\le K \\ j\ne i \end{smallmatrix}}{\mathop{\rm min}}\,\left\{ \frac{D\left( {{C}_{i}},{{C}_{j}} \right)}{\underset{k=1,...,K}{\mathop{\rm max}}\,diam\left( {{C}_{k}} \right)} \right\} \right\},\end{split}\]

   \(D({{C}_{i}},{{C}_{j}})=\underset{x\in {{C}_{i}},y\in {{C}_{j}}}{\mathop{\rm min}}\,d\left( x,y \right)\) jest minimalną odległością pomiędzy obiektami grup \({{C}_{i}}\) oraz \({{C}_{j}}\), natomiast \(diam\left( {{C}_{k}} \right)=\underset{x,y\in {{C}_{i}}}{\mathop{\rm max}}\,\left\{ d\left( x,y \right) \right\}\) jest średnicą grupy \(C_i\). W przypadku, gdy w zbiorze danych występują zwarte, dobrze rozdzielone grupy, odległości między grupami są stosunkowo wysokie, a średnice grup małe. Daje to w rezultacie wysokie wartości indeksu Dunna. Optymalna liczba grup odpowiada maksimum omawianego indeksu. Indeks jest wrażliwy na obiekty odstające i liczony jest w oparciu o twardy podział.

2. Indeks Daviesa-Bouldina:

   \[DB\left( K \right)=\frac{1}{K}\sum\limits_{i=1}^{K}{\left( \underset{j=1,...,K\wedge i\ne j}{\mathop{\rm max}}\,\left\{ \frac{{{w}_{i}}+{{w}_{j}}}{D\left( {{C}_{i}},{{C}_{j}} \right)} \right\} \right)}\]

   \(D\left( {{C}_{i}},{{C}_{j}} \right)\) jest miarą odległości między grupami \(C_i\) oraz \(C_j\), natomiast \(w_i:math:\) dla \(i=1,...,K\) oznaczają wagi grup. Indeks polega na wyliczeniu średniej wartości podobieństwa między grupami. Oczekuje się, by podobieństwo między grupami było jak najmniejsze dlatego optymalna liczba grup minimalizuje powyższy indeks.

3. Indeks SD:

   \[SD\left( K \right)=\alpha Scat\left( K \right)+Dis\left( K \right),\]

   \(Scat\left( K \right)=\frac{1}{K}\sum\limits_{k=1}^{K}{\frac{\left\| {{\sigma }_{k}} \right\|}{\left\| \sigma \right\|}}\) oraz \(Dis\left( K \right)=\frac{\underset{i,j=1,...,K}{\mathop{\rm max}}\,\left\| {{c}_{i}}-{{c}_{j}} \right\|}{\underset{\begin{smallmatrix} i,j=1,...,K \\ i\ne j \end{smallmatrix}}{\mathop{\rm max}}\,\left\| {{c}_{i}}-{{c}_{j}} \right\|}\sum\limits_{k=1}^{K}{{{\left( \sum\limits_{j=1}^{K}{\left\| {{c}_{k}}-{{c}_{j}} \right\|} \right)}^{-1}}}\), \({{\sigma }_{k}}\) dla \(k=1,...,K\) oznacza wektor odchyleń standardowych cech w \(k\)-tej grupie, a \(\sigma\) wektor odchyleń standardowych cech w całym zbiorze danych. Pierwszy składnik sumy oznacza średnie rozproszenie wewnątrz grup, natomiast drugi miarę ogólnej separacji między grupami liczony na podstawie ich prototypów (środków grup \({{c}_{k}}\)), a ich udział w indeksie ważony jest stałą \(\alpha\). Za optymalną liczbę grup przyjmujemy tą, która minimalizuje wartość omówionego indeksu.

Indeksy 1-4 zdefiniowane są dla podziału twardego, w literaturze istnieje również szereg indeksów, które obliczamy w oparciu o rozmytą macierz podziału. W przypadku stosowania algorytmów grupowania rozmytego powyższe indeksy również mogą być stosowane po dokonaniu wyostrzania. Załóżmy, że podział na \(K\) grup wyznaczony jest przez rozmytą macierz podziału \(U=\left[ {{u}_{ij}} \right]\) \(\text{dla }i=1,...,K,j=1,...,N\). Poniżej podajemy przykładowe indeksy względne obliczane na podstawie macierzy rozmytego podziału.

1. Indeks podziału (ang. partition coefficient):

   \[PC\left( U \right)=\frac{1}{N}\sum\limits_{i=1}^{K}{\sum\limits_{j=1}^{N}{u_{ij}^{2}}}\]

   przyjmujący wartości z zakresu \(\left[ 1/K,1 \right]\), im bliższy jedynce tym podział jest bliższy twardemu, a im bliższy wartości \(1/K\) tym bardziej rozmyty i większe prawdopodobieństwo, że w zbiór nie ma struktury złożonej z \(K\) grup. Dla optymalnej liczby grup omawiany współczynnik powinien mieć zatem wartość możliwie bliską jedynce.

2. Indeks Xie-Beni:

   \[\left( U \right)=\frac{\sum\limits_{k=1}^{N}{\sum\limits_{i=1}^{C}{{{\left( {{u}_{ik}} \right)}^{m}}d_{{}}^{2}\left( {{c}_{i}},{{x}_{j}} \right)}}}{N\left( \min {{\left\| {{c}_{i}}-{{c}_{j}} \right\|}^{2}} \right)}\]

   gdzie \({{c}_{i}}\) dla \(i=1,...,K\) oznaczają środki grup, a ich sposób wyliczania jest identyczny jak w przypadku algorytmu FCM. Im mniejsza wartość przedstawionego indeksu, tym grupy wyznaczone przez rozmyta macierz podziału są bardziej zwarte i odseparowane od siebie. Optymalna liczba grup minimalizuje wartość indeksu Xie-Beni.

Przykład 21

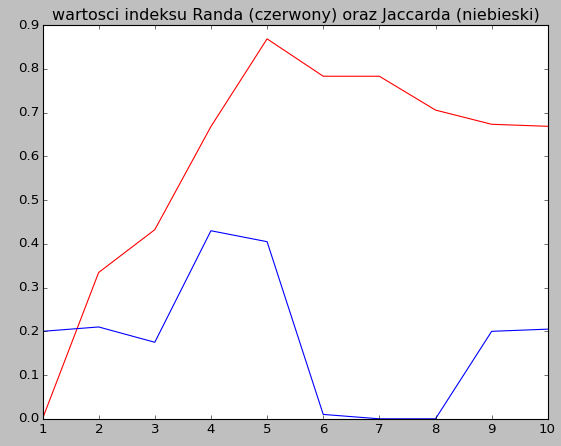
W tym przykładzie dokonamy obliczenia dwóch przykładowych indeksów walidacyjnych: indeksu Randa oraz Jaccarda dla porównania uzyskanego za pomocą algorytmu k-średnich podziału wygenerowanego zbioru danych z założoną strukturą tego zbioru, to znaczy z etykietami zgodnymi ze sposobem jego generowania. W założeniu generowany zbiór składa się z 300 elementów z przestrzeni 3-wymiarowej i liczy 5 skupień. Dokonujemy podziału tego zbioru w zakresie 1-10 grup za pomocą algorytmu k-średnich i obliczamy wspomniane indeksy. Na największe podobieństwo obydwu podziałów wskazuje maksymalna uzyskana wartość wspomnianych indeksów. Ich wartości umieszczamy na wykresie oczekując że wartość maksymalną znajdziemy dla \(k=5\) grup. Przykładowy wykres umieszczony został na rysunku 1.

Rysunek 1: Wartości indeksu Randa oraz Jaccarda. Źródło: opracowanie własne

Zgodnie z nim za najbliższy założonemu zgodnie z indeksem Randa zostaje wybrany podział na 5 grup, natomiast zgodnie z indeksem Jaccarda na 4 grupy. Poniższy skrypt realizuje to zadanie.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn import datasets
from sklearn.datasets import make_classification
from sklearn.metrics import adjusted_rand_score, jaccard_similarity_score

#Wygenerowanie zbioru danych na potrzeby klasyfikacji
mk_data=make_classification(n_samples=200, n_features=3, n_informative=3,
                         n_redundant=0, n_repeated=0, n_classes=5,
                         n_clusters_per_class=1, class_sep=2.5)
#dane uczące
Data=mk_data[0]
#etykiety - na potrzeby wygenerowania macierzy konfuzji
Classes=mk_data[1]

#ilustracja zbioru danych za pomocą wykresu 3D
fig = plt.figure(1)
wykr = Axes3D(fig)
plt.title('Wygenerowany zbior danych')
wykr.scatter(Data[:, 0], Data[:, 1], Data[:, 2])
plt.show()

rand_ind=[]
jacc_ind=[]
for i in range(1,11):
    kmeans=KMeans(n_clusters=i)
    #uczenie algorytmu kMeans
    kmeans.fit(Data)

    #uzyskany podział
    podzial=kmeans.labels_

    #Wartości indeksu Randa oraz Jaccarda
    rand_ind.append(adjusted_rand_score(podzial,Classes))
    jacc_ind.append(jaccard_similarity_score(podzial, Classes))

plt.title('wartosci indeksu Randa (czerwony) oraz Jaccarda (niebieski)')
plt.plot(range(1,11),rand_ind,c='r')
plt.plot(range(1,11),jacc_ind,c='b')
plt.show()