Interfejs pomiarowy do generacji i akwizycji napięć zmiennych¶
Cel ćwiczenia¶
Celem ćwiczenia jest wykonanie interfejsu pomiarowego do generowania i akwizycji napięć zmiennych oraz wykonywania charakterystyk częstotliwościowych z wykorzystaniem LabVIEW i układu NI my DAQ.
Wymagane wiadomości¶
Podstawy programowania w środowisku LabVIEW. Obsługa interfejsu pomiarowego NI MyDAQ. Napięcie sinusoidalnie zmienne, jego amplituda, wartość skuteczna, napięcie międzyszczytowe, częstotliwość. Sygnały stosowane w elektronice i ich podstawowe parametry. Poziom sygnału, skala decybelowa względna i bezwzględna. Charakterystyka amplitudowa i fazowa. Pasmo przenoszenia. Generator funkcji i jego obsługa.
Charakterystyki częstotliwościowe¶
Jedną z podstawowych metod określania właściwości układów dynamicznych jest wyznaczanie ich charakterystyk częstotliwościowych. Charakterystyka częstotliwościowa opisuje odpowiedź układu na wymuszenie harmoniczne (sinusoidalne) o częstotliwości zmieniającej się w określonym zakresie (charakter fizyczny sygnału wejściowego i wyjściowego może być różny). Sygnał harmoniczny jest szczególnie przydatny jako sygnał testowy z kilku powodów:
- każdy sygnał (skończony lub okresowy) może być wyrażony jako suma sygnałów sinusoidalnych o różnych częstotliwościach (rozkład sygnału na szereg Fouriera),
- odpowiedź stacjonarnego stabilnego układu liniowego na wymuszenie sinusoidalne jest sinusoidą o tej samej częstotliwości,
- przebieg sinusoidalny jest łatwy do wygenerowania.
Dwa pierwsze fakty wskazane powyżej oraz zasada superpozycji sprawiają, że odpowiedź liniowego układu stacjonarnego na dowolne wymuszenie można wydedukować na podstawie jego charakterystyki częstotliwościowej (dla przykładu, jakość sygnału wyjściowego wzmacniacza audio ocenia się na podstawie jego charakterystyki częstotliwościowej, chociaż sygnały dźwiękowe nie są sinusoidalne).
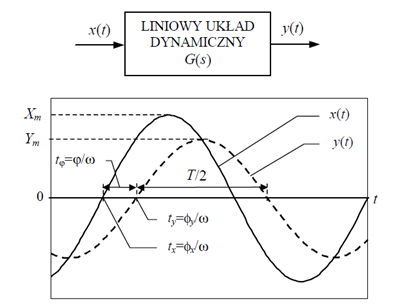
Rysunek 1: Sygnał harmoniczny przed i po przejściu przez liniowy układ dynamiczny [aislab]
Jeżeli na wejście liniowego układu dynamicznego podamy sygnał sinusoidalny \(x(t) = X_m cos(\omega t +\phi_x )\) to po zaniknięciu procesów przejściowych na wyjściu układu otrzymamy również sygnał sinusoidalny \(y(t) = Y_m cos(\omega t +\phi_y )\) o tej samej częstotliwości kołowej (pulsacji) \(\omega=2\pi f [rad/s]\), ale w ogólności o innej amplitudzie i fazie (rys. 1), przy czym zmiana amplitudy i fazy sygnału po przejściu przez układ jest różna dla różnych wartości \(\omega\). Charakterystyka amplitudowa \(A(\omega)\) jest to stosunek amplitudy sygnału wyjściowego do amplitudy sygnału wejściowego (wzmocnienie układu) w funkcji częstotliwości \(\omega\):
Charakterystyka fazowa \(\phi(\omega)\) jest to przesunięcie fazowe (podawane w stopniach lub radianach) sygnału wyjściowego w stosunku do sygnału wejściowego w funkcji częstotliwości \(\omega\):
Przy zdejmowaniu charakterystyki częstotliwościowej amplituda sygnału wejściowego jest zwykle utrzymywana na stałym poziomie \(X_m(\omega)=X_m=const\). W praktyce korzysta się z charakterystyk częstotliwościowych wyznaczonych w skali logarytmicznej, nazywanymi charakterystykami Bodego. Logarytmiczna charakterystyka amplitudowa \(Lm(\omega)\) (logarytmiczny moduł wzmocnienia) jest określona zależnością:
i podawana w decybelach [dB] wzmocnienia zdefiniowanego wzorem (1) w funkcji częstotliwości przedstawionej w skali logarytmicznej, Logarytmiczna charakterystyka fazowa \(\phi(\omega)\) jest zależnością przesunięcia fazowego od częstotliwości przedstawionej w skali logarytmicznej. Para charakterystyk Bodego przedstawia zależność logarytmu wzmocnienia i przesunięcia fazowego od częstotliwości w sposób jawny. Jeżeli znany jest model matematyczny liniowego układu dynamicznego w postaci transmitancji operatorowej \(G(s)\), to na podstawie \(G(s)\) można wyznaczyć charakterystyki częstotliwościowe układu. W tym celu określa się tzw. transmitancję widmową:
Transmitancja widmowa jest szczególnym przypadkiem transmitancji operatorowej obliczanej na osi urojonej \(s=j\omega\) na płaszczyźnie zmiennej zespolonej (oznacza to zastosowanie zespolonego przekształcenia Fouriera zamiast przekształcenia Laplace’a). Zależność modułu transmitancji widmowej \(G(j\omega)\) od częstotliwości \(\omega\) jest charakterystyką amplitudową układu, a zależność argumentu od częstotliwości – charakterystyką fazową:
Innym ze sposobów przedstawiania właściwości częstotliwościowych układu j est wykres parametryczny (względem parametru \(\omega\)) jego transmitancji widmowej na płaszczyźnie zespolonej nazywany wykresem Nyquista. Jest on linią zakreślaną na płaszczyźnie zespolonej przez koniec wektora \(G(j\omega)\) przy zmianie \(\omega\) od \(0\) do \(\infty\) (tzw. hodograf). Procedury komputerowe wyznaczające charakterystykę na podstawie transmitancji mogą rysować wykres również dla ujemnych wartości \(\omega\). W takim przypadku połowa wykresu dla \(\omega<0\) jest symetrycznym odbiciem względem osi rzeczywistej hodografu dla \(\omega>0\) (ze względu na symetrię funkcji \(G(j\omega)\). Ponieważ wykres zawiera informacje zarówno o wzmocnieniu jak i o przesunięciu fazowym, nazywa się go charakterystyką amplitudowo-fazową. Niejawny rozkład częstotliwości wzdłuż linii określa się przez podanie jej wartości w ważniejszych punktach (np. w punktach przecięcia wykresu z osiami współrzędnych).
Przebieg ćwiczenia¶
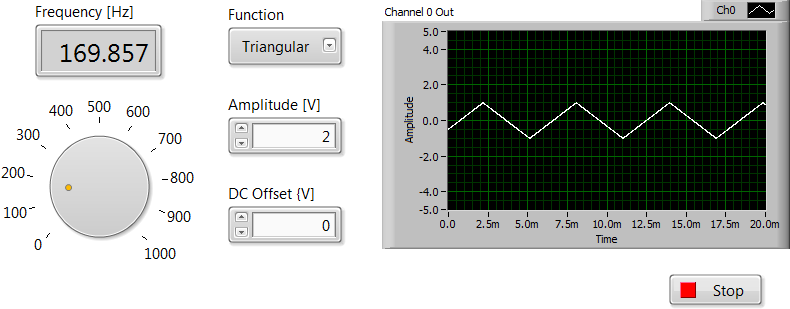
Generator funkcji Zbuduj w oparciu o urządzenie NI myDAQ aplikację pełniącą rolę generatora funkcji. Panel sterujący ww. urządzenia znajduje się na rys. 2.
W aplikacji należy skorzystać między innymi z kontrolek znajdujących się w zakładce NI ELVISmx (NI ELVISmx Osciloscope, NI ELVISmx Function Generator). Po napisaniu aplikacji sprawdzić wspólnie z prowadzącym zajęcia jej działanie uprzednio wykonując połączenia punktów wyjścia generatora (kanał AO \(0\)) z jednym z wejść oscyloskopu (kanały AI \(0+\) /AI \(1+\)). Na panelu sterującym (Front Panel) powinna znajdować się, także informacja o autorze programu oraz nazwa programu związana z wykonywanym punktem ćwiczenia.
Charakterystyka amplitudowa i fazowa Zbuduj w oparciu o urządzenie NI myDAQ aplikację pozwalającą na pomiar charakterystyk amplitudowej i fazowej danego układu. Panel sterujący ww. urządzenia znajduje się na rys. 3.
W aplikacji należy skorzystać między innymi z kontrolek znajdujących się w zakładce NI ELVISmx (NI ELVISmx Osciloscope, NI ELVISmx Function Generator) oraz z kontrolki Extract Single Tone Information.vi (Programing…Waveform Measurements). Po napisaniu aplikacji sprawdzić wspólnie z prowadzącym zajęcia jej działanie uprzednio wykonując połączenia punktów wyjścia generatora (kanał AO \(0\)) z kanałami wejściowymi oscyloskopu (kanały AI \(0+\) i AI \(1+\)). Za pomącą napisanej aplikacji wykonać pomiary charakterystyk częstotliwościowych dla filtru dolnoprzepustowego pierwszego rzędu o \(fg=200Hz\). Podobnie jak w poprzednim punkcie na panelu użytkownika (Front Panel) powinna znajdować się, także informacja o autorze programu oraz nazwa programu związana z wykonywanym punktem ćwiczenia.
Opracowanie wyników
Sprawozdanie powinno zawierać:
- Zrzut z ekranu komputera paneli sterujących napisanych aplikacji.
- Kod napisanych programów wraz z opisem.
- Opis praktycznego zastosowania napisanych aplikacji.
- Z otrzymanych przykładowych charakterystyk częstotliwościowych wykonać charakterystykę amplitudowo - fazową (wykres Nyquista).
- Porównać otrzymane charakterystyki częstotliwościowe z zależnościami teoretycznymi.
Literatura¶
| [Tlaczala2010-3] | W. Tłaczała, Środowisko LABVIEW w eksperymencie wspomaganym komputerowo, WNT W-wa 2010, |
| [Tietze1999-3] | U. Tietze, Ch. Schenk, Układy półprzewodnikowe, WNT W-wa 1999, |
| [Pioro1996-3] | B. Pióro, Podstawy elektroniki, część I i część II, Warszawa 1996, |
| [aislab] | http://www.ztmapc.el.pcz.pl/stud/ais/aislab-cf.pdf |
Testy do rozdziału¶
Test 1¶
Test 2¶
Pytania kontrolne¶
- Co nazywamy charakterystyką widmową układu?
- Charakterystyka amplitudowa przedstawia zależność…
- Charakterystyka fazowa przedstawia zależność…
- Wzmocnienie układu wynosi 20 dB. Ile wynosi rzeczywiste wzmocnienie tego układu?
- Jakie układy nazywamy układami liniowymi?
- Co przedstawia charakterystyka Bodego?
- Na jakiej płaszczyźnie wykreśla się wykres Niquista?
- Co przedstawia wykres Niquista?
- Dlaczego charakterystyki amplitudową oraz fazową wykreśla się w skali logarytmicznej?
- Jakiego sygnału używamy do wyznaczenia charakterystyk częstotliwościowych danego układu?