Układy funkcyjne- realizacja dowolnych funkcji logicznych za pomocą bramek logicznych¶
Cel ćwiczenia¶
Celem ćwiczenia jest poznanie realizacji funkcji logicznych przy pomocy podstawowych funktorów z szeregu cyfrowych układów scalonych TTL i CMOS oraz projektowanie i budowa układów logicznych powszechnie stosowanych w automatyce i technice cyfrowej.
Wymagane wiadomości¶
Znajomość budowy funkcji logicznych przy pomocy bramek logicznych w technologii TTL i CMOS, umiejętność stosowania kodów cyfrowych i praw techniki cyfrowej.
Prawa techniki cyfrowej¶
Zmienne logiczne przyjmują dwie wartości dyskretne:
- zero logiczne: „0” lub „L”
- jedynka logiczna: „1” lub „H”
Podstawowe działania, związki pomiędzy zmiennymi logicznymi:
- iloczyn (koniunkcja): \(y=x_1\land x_2=x_1x_2\)
- suma (dysjunkcja): \(y=x_1\lor x_2=x_1+x_2\)
- negacja: \(y=\sim x=\overline{x}\)
Algebra Boole’a, prawa obowiązujące w.w. działaniach:
przemienności: \(x_1+x_2=x_2+x_1\) oraz \(x_1x_2=x_2x_1\);
łączności: \((x_1+x_2)+x_3= x_1+(x_2+x_3)\) oraz \((x_1x_2)x_3= x_1(x_2x_3)\);
rozdzielczości: \((A+B)C=AC+BC\ oraz :math:`AB+C=(A+C)(B+C)\);
pochłaniania: \(A(A+B)=A\) oraz \(A+AB=A\);
prawa de Morgana: \(\sim (AB)=\sim A+\sim B\) \(\sim (A+B)=\sim A\land \sim B\)
wzory Boole’a:
\[A+A=A \text{ oraz } AA=A\]\[A+1=1 \text{ oraz } A\land 1=A\]\[A+0=A \text{ oraz } A\land 0=0\]\[A+\sim A=1 \text{ oraz } A\land\sim A=0\]
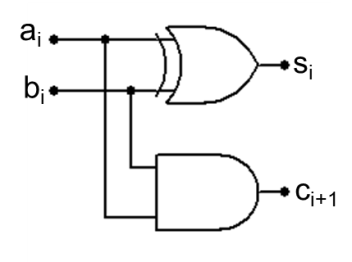
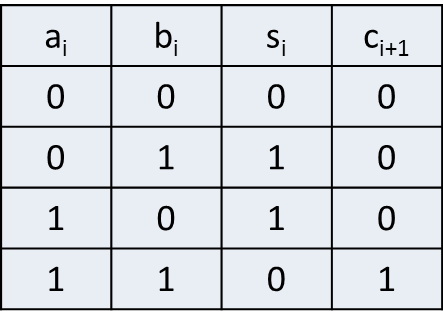
Stosując powyższe prawa można zapisać funkcję logiczną w postaci kanonicznej niezależnie od symboliki argumentów (\(X_1\) lub \(A\)). Do opisu działania bramek logicznych stosuje się tzw. tablice prawdy. Zawiera ona wszystkie kombinacje sygnałów wejściowych, oraz odpowiadający im stan na wyjściu bramki. Realizację funkcji logicznych przy pomocy bramek można przedstawić także językiem algebry Boole’a, której działania opisane są powyżej. Stosując tą terminologię możemy zrealizować każdą funkcje logiczna tworząc takie układy jak przedstawione poniżej sumator i subtraktor, które realizują konkretną funkcje kilku argumentów posiadając dwa wyjścia zależne od argumentów wejściowych. Rozróżnia się układ zwany sumatorem rys. 2 od półsumatora rys. 1 gdyż oba posiadają dwa wyjścia jednak w sumatorze uwzględnione jest wejście przeniesienia z poprzedniej pozycji sumowania. Dzięki takiej postaci możemy wykonać dodawanie arytmetyczne rys. 2 oraz odejmowanie arytmetyczne rys. 3 opisane funkcjami poniżej.
Półsumator jednobitowy¶
 |
|
 |
|
 |
|
\(s_i=\overline{a_i}b_i+a_i\overline{b_i}=a\oplus b_i\) \(c_{i+1}=a_ib_i\) |
Rysunek 1: a) Symbol, b)schemat realizacji, c)tabela prawdy, d)funkcja opisująca działanie układu
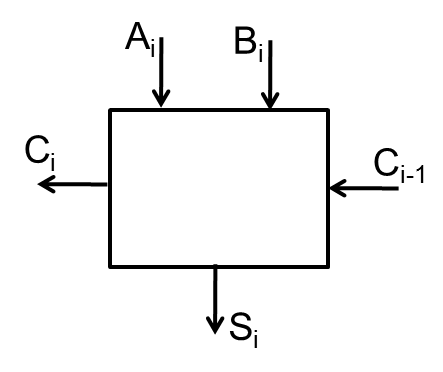
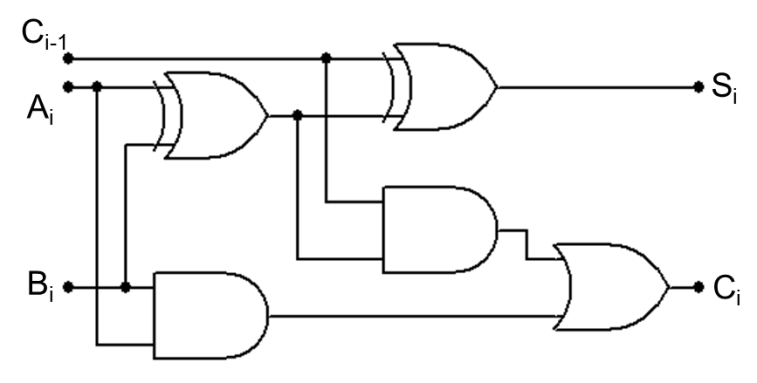
Sumator jednobitowy¶
 |
|
 |
|
 |
|
\(S_i=\overline{C_{i-1}}\overline{A_{i}}B_i+\overline{C_{i-1}}+A_i\overline{B_{i}}+C_{i-1}\overline{A_{i}}\overline{B_{i}}+C_{i-1}A_iB_i\) \(C_i=A_iB_i+C_{i-1}B_i+C_{i-1}A_i\) |
Rysunek 2: a) Symbol, b)schemat realizacji, c)tabela prawdy, d)funkcja opisująca działanie układu
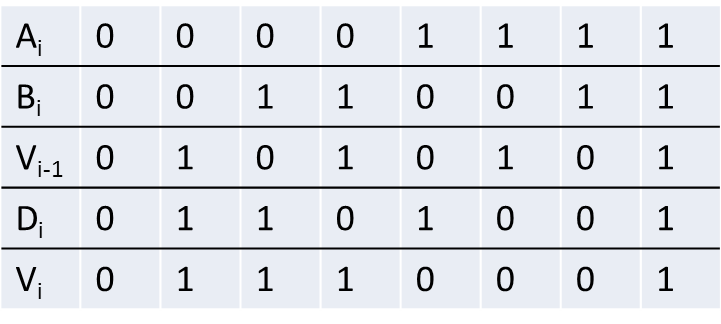
Subtraktor jednobitowy¶
 |
|
 |
|
\(D_i=\overline{V_{i-1}}\overline{A_{i}}B_i+\overline{V_{i-1}}+A_i\overline{B_{i}}+V_{i-1}\overline{A_{i}}\overline{B_{i}}+V_{i-1}A_iB_i\) \(V_i=A_iB_i+V_{i-1}B_i+V_{i-1}A_i\) \(V_i=\overline{A_i}B_i+V_{i-1}(\overline{A_i}\oplus +B_i)\) |
Rysunek 3: a) Symbol, b)tabela prawdy, c)funkcja opisująca działanie układu
Przebieg ćwiczenia¶
Realizacja elementarnych funkcji boolowskich
Zrealizować następujące funkcje przy użyciu tylko bramek NAND i sporządzić dla nich tablicę zależności. Do praktycznej realizacji funkcji wykorzystać środowisko LabVIEW lub CEDAR Logic. Każdą funkcje przedstawioną poniżej w postaci kanonicznej zminimalizuj i dokonaj transformacji do postaci realizacji za pomocą bramek NAND. Wykonaj symulacje funkcji wprost godnie z zapisem kanonicznym i po transformacji.
- \(y(X_1X_2X_3X_4)=X_1X_2X_3X_4+X_1X_2\overline{X_3}X_4+\overline{X_1}\overline{X_2}X_3X_4+X_1X_2\overline{X_3}\overline{X_4}\)
- \(y(X_1X_2X_3)=X_1X_2X_3+X_1\overline{X_2}X_3+\overline{X_1}\overline{X_2}X_3\)
- \(y(X_1X_2X_3)=(X_1+X_2)(\overline{X_1}+\overline{X_3})(X_2+X_3)\)
- \(y(X_1X_2X_3)=(\overline{X_1+X_2})X_2\overline{X_3}+\overline{X_1}\overline{X_2}\overline{X_3}+(\overline{X_2}\overline{X_3}+X_2X_3)X_1\)
Badanie elementarnych funkcji boolowskich
- Znaleźć wyrażenie opisujące pracę półsumatora i sumatora 1 bitowego, zaprojektować jego układ logiczny tylko za pomocą bramek NAND. Sporządzić tablicę zależności badanego sumatora.
- Znaleźć wyrażenie opisujące pracę układu różnicy liczb 1 bitowych, zaprojektować jej układ logiczny tylko za pomocą bramek NAND i sporządzić tablicę zależności.
Wyniki pomiarów i schematy przenieść na karty pomiarowe, pomiary wykonać w środowisko LabVIEW lub CEDAR Logic. Wykonując ten punkt należy wzorować się na opisie powyżej i tabelach działania sumator i subtraktora.
Opracowanie wyników¶
W sprawozdaniu:
- Sporządzić schematy badanych funkcji przy pomocy bramek logicznych wraz z tabelą działania dla przebadanych funkcji.
- Sporządzić schematy badanych układów z użyciem sumatora i subtaktora wraz z tabelą działania.
Literatura¶
| [Filpkowski2005-2] | A. Filpkowski, „Ukady elektroniczne analogowe i cyfrowe” EIT 2005r. |
| [Kalisz2002-2] | J. Kalisz, „Podstawy elektroniki cyfrowej” WKŁ 2002r |
| [Horowitz2002-2] | P. Horowitz, W Hill, „Sztuka elektroniki” WKŁ 2002r. |
| [Pioro2005-2] | M. Pióro, „Podstawy elektroniki” WSiP 2005r. |
| [Chwaleba2002-2] | A. Chwaleba, „Pracownia elektroniczna” WSiP 2002r. |
| [Pioro1996-7] | M. Pióro „Podstawy elektroniki, część I i część II”, Warszawa 1996, |
| [Piecha1985-2] | J. Piecha, „Elementy cyfrowe TTL” Skrypt Uniwersytetu Śląskiego 1985 |
Testy do rozdziału¶
Test 1¶
Test 2¶
Test 3¶
Test 4¶
Test 5¶
Test 6¶
Test 7¶
Test 8¶
Test 9¶
Test 10¶
Pytania kontrolne¶
- Jakie wejście w półsumatorze realizuje przeniesienie z pozycji poprzedniej
- Podaj funktor logiczny który realizuje funkcję półsumatora
- Czy wyjście \(C_{i+1}\) da się opisać funktorem logicznym
- Jakie urządzenie wybiera 1 wejście z N i przekazuje wynik na wyjście zgodnie z przydzielonym adresem
- Czy sumator przypisuje 1 wejście do 1 wyjścia
- Jaki wynik otrzymamy realizując działanie logiczne \(A+1=\)
- Jaki wynik otrzymamy realizując działanie logiczne \(A+0=\)
- Jaki wynik otrzymamy realizując działanie logiczne \(A+\sim A=\)
- Ile rozwiązań funkcji trójargumentowej można zrealizować za pomocą sumatora
- Ile rozwiązań funkcji trójargumentowej można zrealizować za pomocą subtraktora